What is parts: Definition and 838 Discussions

In science and engineering, the parts-per notation is a set of pseudo-units to describe small values of miscellaneous dimensionless quantities, e.g. mole fraction or mass fraction. Since these fractions are quantity-per-quantity measures, they are pure numbers with no associated units of measurement. Commonly used are parts-per-million (ppm, 10−6), parts-per-billion (ppb, 10−9), parts-per-trillion (ppt, 10−12) and parts-per-quadrillion (ppq, 10−15). This notation is not part of the International System of Units (SI) system and its meaning is ambiguous.

View More On Wikipedia.org
Recent contents Top users
  1. Greg Bernhardt

    What is Integration By Parts? A 5 Minute Introduction

    Continue reading...
  2. I

    MHB Sony Vaio Parts: Cover Lids & Rubber Feet

    where can i get a cover lid for a 14.5" sony vaio. or the little rubber feet for sony vaio pcg-61611L
  3. E

    Integration by Parts Evaluate the integral

    Homework Statement Evaluate the integral. (Use C for the constant of integration.) ∫te ^ (-9t) dtHomework Equations ∫udv = uv - ∫vdu u=t dv= e ^ (-9t) dt du=dt v=(-1/9) e ^(-9t) The Attempt at a Solution = -1/9 te^(-9t) - ∫-1/9 e ^(-9t) dt Second Integral...
  4. I

    MHB Integration by Parts: Solve $$\frac{xe^{2x}}{(1+2x)^2}$$

    Im supposed to use integration by parts for this problem but i understand how to. $$\int \ \frac{xe^{2x}}{(1+2x)^2},dx$$
  5. B

    Integration by Parts To Derive Expectation Value of Velocity

    Homework Statement Why can't you do integration-by-parts directly on the middle expression in equation 1.29--pull out the time derivative over onto x, note that \displaystyle \frac{\partial x}{\partial t} = 0, and conclude that \displaystyle \frac{d \langle x \rangle }{dt} = 0Homework Equations...
  6. J

    Is this a valid operation (integration by parts)?

    Say I have a function, f(x) = x sec (f(x)) [this is just an example function, the actual problem is more complicated] g(x) = x f(x), then using integration by parts, I can write I = a∫bg(x) dx = a∫bx f(x) dx = (f(x) \frac{x^{2}}{2})|^{b}_{a}- \frac{1}{2}a∫b\frac{d f(x)}{dx} x2 dx...
  7. K

    Machine Parts requiring cleaning in Steel Mills?

    Hello all! I have recently started a Parts Cleaning Machine manufacturing business. Most of my clients are Automobile Manufacturers & Ancillaries. The last couple of years have been disastrous for the automobile industry here. So I was looking to broaden my horizon and target the Steel...
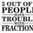
  8. DreamWeaver

    MHB A Dilogarithmic integration by parts

    From the logarithmic integral representation of the Dilogarithm, \text{Li}_2(x), |x| \le 1, prove the reflection formula for the Dilogarithm. Dilogarithm definition:\text{Li}_2(x) = -\int_0^1\frac{\log(1-xt)}{t}\, dt = \sum_{k=1}^{\infty}\frac{x^k}{k^2}Dilogarithm reflection...
  9. L

    MHB Integral by Parts: Solving 2 Integrals Involving Arctg(x) & Sqrt(1-x^2)

    integral of arctg(x)/sqrt(1-x^2) maybe u = arctg x du = 1 /1+x^2 but x = tg u maybe this is the way isn't it?
  10. L

    MHB Solve Integral by Parts: exsqrt(x)

    integral is exsqrt(x) ok here u = sqrt(x) du = 1/(2sqrt(x)) dv ex= v= ex so exsqrt(x) - integral( 1/2sqrt(x)ex) And I can't continue because i can not get rid of ex?? How must I proceed??
  11. H

    Integration by Parts and Series

    This isn't really a homework question, more just something I noticed while evaluating an integral and was curious about: At this stage, I was able to simplify the expression before solving for the integral algebraically (since the second iteration yielded the original integral the right...
  12. U

    Intergration by parts for sin(x)cos(x)

    I know its easier to use the substitution method, by I'm trying to see how it'll work for integration by parts. I follow the LIATE method for integration by parts. Now if I take u=cos(x) and dv = sin(x), the answer changes. Can you please explain this to me? Which is the 'right'...
  13. B

    Rotating parts of a motor have a moment of inertia

    Homework Statement The rotating parts of a motor have a moment of inertia of 15 kgm^2 and an optimum running speed of 1400 rev/min. When operating the motor is connected at optimum speed , by means of a clutch, to a shaft which has a counter rotation of 600 rev/min. The shaft has a mass of...
  14. T

    What Is the Probability of Rejecting a Batch with Defective Components?

    Homework Statement A manager must assess the quality of a new batch of 25 components ready for shipping. Rather than assess each component, a sample of 5 is randomly selected and tested. The quality control speci fication is that if there are 2 or more defectives in the sample, the...
  15. E

    How do you know when to use substituion or integration by parts?

    When you have a fraction, how do you know when to use iteration by parts, or use substituion, pick a u, solve for a value of x (like x=u-2) and then plug in those values?
  16. L

    MHB Integrating xarctg2x Using Integration by Parts

    it is integral of xarctg2x u = arctg2x du =1/(1+x2) or 2(arctgx/(1+x2) ?' I am stuck here dv = x v =x2/2
  17. T

    Proof Involving Integration by Parts and a Series of Functions

    Homework Statement Let f be continuous on an interval I containing 0, and define f1(x) = ∫f(t)dt, f2(x) = ∫f1(t)dt, and in general, fn(x) = ∫fn-1(t)dt for n≥2. Show that fn+1(x) = ∫[(x-t)n/n!]f(t)dt for every n≥0. ALL INTEGRALS DEFINED FROM 0 to x (I can't format :( ) Homework...
  18. U

    Integration by Parts Homework: Get Help Now

    Homework Statement Homework Equations N/A The Attempt at a Solution I can't even begin the attempt because I don't know how you could use intergration by parts for this sum in the first place. Can you help me out?
  19. L

    MHB What is the meaning of Si in the integral of ln(x)cos(x)?

    integral ln(x).cos(x) Here I have some clear ideas U = lnx du = 1/x dv = cosx so int de cosx = v = -sinx -sinxlnx -int (sinx)/(x) Ok I think I must integrate again u= sinx du = cosx dv = 1/x v = lnx Again I got -sinxlnx -int (sinx lnx) But I am stuck here and I don't know how to...
  20. F

    Integration by parts with orthogonality relation

    Homework Statement I want to integrate \int_{0}^{a} xsin\frac{\pi x}{a}sin\frac{\pi x}{a}dxHomework Equations I have the orthogonality relation: \int_{0}^{a} sin\frac{n\pi x}{a}sin\frac{m\pi x}{a}dx = \begin{cases} \frac{a}{2} &\mbox{if } n = m; \\ 0 & \mbox{otherwise.} \end{cases} and...
  21. I

    How to integrate by parts when del operator is involved?

    i'm trying to integrate this: $$W=\frac{ε}{2}\int{\vec{∇}\cdot\vec{E})Vdτ}$$ where ε is a constant, E= -∇V, τ is a volume element how do i end up with the following via integration by parts? $$W=\frac{ε}{2}[-\int{\vec{E}\cdot(\vec{∇}V)dτ}+\oint{V\vec{E}\cdot d\vec{a}}$$] where the vector a...
  22. Yae Miteo

    Integration by parts with e and sine

    Homework Statement Evaluate the integral. Homework Equations \int e^{2x} sin(3x) dx The Attempt at a Solution I began by using integration by parts. u = sin(3x) v = \frac {e^{2x}} {2} du = 3 cos(3x) dv = e^{2x} dx but I get stuck after that because the...
  23. O

    Integration by Parts confusions

    Hi all ! I'm new here :) So I'm facing some confusions here regarding integration by parts. While surfing through the internet to study more about this topic, I've came across two formulas which are used in solving problems related to integration by parts. They are 1. uv - ∫uv'dx 2. uv -...
  24. M

    Electric Potential Energy in Different parts of Circuit

    When a positive charge leaves the positive part if the battery it has maximum electric potential energy then as it moves through a wire with a zero resistance the charge is closer to the negative side of the battery. So, while traveling in a wire in a circuit does it lose electric potential...
  25. G

    What are the Alternative Parts for L14F1,LD271 & S20102

    What are the Alternative Parts for Transistor (L14F1) Diode (LD271) IC (S20102) While I was surfing the net in the hope of finding a Solution to this, I found a Thread Regarding the same in this Site, It was Very Helpful, But not mention the part name (code) wise, I am a newbie to...
  26. F

    Integration - Indefinite - By Parts and U-Sub

    Homework Statement Integrate the following indefinite integrals A:\int e^x (x^2+1) dx B:\int e^x cos(3x+2) dxHomework Equations \int u dv = uv - \int v du The Attempt at a Solution Part A: I have done the following but when I use an integration calculator online its not what I have (although...
  27. D

    Why do bound systems have less rest mass than the sum of its parts?

    Hi PF. This a fact well aware to just about anyone that has had even basic chemistry, but I'm having a hard time coming to an understanding as to why this must be true. So why? Also, if I knew that some box contained, say, a proton and an electron, could I ever know whether or not, inside...
  28. S

    Substitution and Integration by Parts

    Homework Statement First make a substitution and then use integration by parts to evaluate the integral. ∫x^{7}cos(x^{4})dx Homework Equations Equation for Substitution: ∫f(g(x))g'(x)dx = ∫f(u)du Equation for Integration by Parts: ∫udv = uv - ∫vdu The Attempt at a Solution So...
  29. S

    Integration by Parts 5x ln(4x)dx

    Homework Statement Use integration by parts to evaluate the integral. ∫5x ln(4x)dx Homework Equations ∫udv = uv - ∫vdu The Attempt at a Solution So here's my solution: But the computer is telling me I'm wrong :( We haven't learned how to integrate lnx yet, so the...
  30. R

    MHB Find angles when circumference is divided into 5 unequal parts

    Hello, I am using a very old textbook from 1895, Loney's Trigonometry, which poses the following problem: If the circumference of a circle be divided into 5 parts, which are in A.P., and if the greatest part be 6 times the least, find in radians the magnitudes of the angles that the parts...
  31. S

    Help with volume of solid of revolution/integration by parts question

    Homework Statement The problem is attached in this post. Homework Equations The problem is attached in this post. The Attempt at a Solution I've set up the integral via disk method: π∫(e^√x)^2 dx from 0 to 1 I've done integration by parts by don't know how to integrate the...
  32. M

    Best way to go for precision aluminum parts?

    I might need to go to a metal shop/fabricator/what have you soon to have work done on a conceptually simple part that has some elements with measurements on the microscopic scale. Think cylinders with a diameter of .2 microns. Lots of them. I would want it done in aluminum. What would be the...
  33. N

    So, what is the problem asking for? Integration by Parts for ∫(z^3e^z)dz

    Homework Statement ∫((z^3)(e^z ))dzHomework Equations I just tried u dv - ∫v duThe Attempt at a Solution u = z^3 dv = e^z du = 3z^2 v = e^z = z^3e^z - ∫(3e^z (z^2)) dz I got this far but after that if I try integration by parts again, it gets too confusing.
  34. jdawg

    Integration by Parts: Solving ∫cosx(lnsinx)dx

    Homework Statement ∫cosx(lnsinx)dx Homework Equations The Attempt at a Solution u=lnsinx dv=cosxdx du=cosx/sinx dx v=sinx =(lnsinx)(sinx)-∫(sinx)(cosx/sinx)dx =(lnsinx)(sinx)-(sinx)+C I thought that I did this correctly, but my teacher said that u should...
  35. A

    MHB Integrate by Parts: Solving (xe^(2x))/((1+2x)^2)

    how do i integrate (xe^(2x))/((1+2x)^2)?? do i substitute 1 + 2x = w? but if i do, how do i proceed from there?
  36. M

    Removing parts of a line (literally)

    Hey pf! I think this is the correct thread. Basically, if I take a line segment and remove half of it, what happens to the point that is in the middle? Also, what happens if I take a segment [0,1] and take [0,1/2) versus [0,1/2]? What length do I have remaining for each of these? Thanks!
  37. M

    Can you use integration by parts?

    How would you integrate this: ## \int x df(x) ## In general, how is this solved: ## \int 1df(x) ## Can you use integration by parts? I tried, but kept getting 0 since I let ## 1 = u## but then ##du = 0## for later purposes. Also, if ## df(x) = u ## then I am still stumped on how to take the...
  38. W

    Drum Brake Parts: What is the Name of the Metal?

    is this a drum brake ? there are a piece of metal sheet assemble to this thing, and what's is the name of the metal?
  39. C

    Find the real and Imaginary parts of sin(3+i)

    Homework Statement Find the real and Imaginary parts of sin(3+i) Homework Equations sin(x+y)= sinxcosy+sinycosx The Attempt at a Solution I think I am right in saying that you use the sine addition formula but then i get stuck from there. Is it something to do with exponential form?
  40. K

    Selection of Pump for Parts Cleaning Machines

    Hello, Budding entrepreneur here looking for help. I've had this doubt for a long time. I can read the pump performance curves with respect to Head & Q. So if I have to select a pump that gives me 200 LPM @ 10 bar pressure, how do I select a pump from the curves. Is selecting a pump that...
  41. K

    Integration of (cosecx)^3 without using integration by parts

    Homework Statement Can anyone help me integrating (cosecx)^3 without using integration by parts? Homework Equations The Attempt at a Solution i couldn't get a clue how to do it,i used fundamental identity but always ended up like [∫(cosecx) dx] + [(∫(cotx)^2 . (cosecx) dx]...
  42. M

    Correct clearance of engine parts

    hello friends,can you explain what is correct clearance of engine's moving parts,giving examples.
  43. MarkFL

    MHB Selena's question at Yahoo Answers regarding a definite integral by parts

    Here is the question: I have posted a link there to this thread so the OP can see my work.
  44. MarkFL

    MHB Anh Nguyen's questions regarding indefinite integrals (integration by parts)

    Here are the questions: I have posted a link there to this thread so the OP can see my work.
  45. MarkFL

    MHB Calc Help: Find b to Divide Region into 2 Equal Areas

    Here is the question: I have posted a link there to this thread so the OP can see my work.
  46. S

    Thought Experiment: The flow of time at different parts of the univers

    Hey all, Just a thought experiement here. With time dilation caused by gravity and relative velocity being a confirmed phenomena, do you think it's possible that other worlds that are extremely far away from each other, and are moving at a very high speeds relative to one another with...
  47. W

    Car Part Names: Identification & Information

    what is the name of this part? what is the name of this component? thank you.
  48. P

    Integration by Parts: Solving an Intricate Integral

    Homework Statement ∫x*cos(x^2) dx I tried using integration by parts, but the integral of cos(x^2) is very long, and I couldn't get it completely with my knowledge at the moment, so is there an easier way to solve this problem?
  49. B

    Integration by parts question.

    Hi guys, Stuck on an integration by parts question...Not going to post the question as I want to work it out myself, but as I'm a bit of a novice on diff/integration I'm stuck on what we do at a certain step of the process...anyway.. I know integration by parts we end up using ∫udv = uv -...
  50. polygamma

    MHB Integration by Parts: Showing $\ln^n(1-x)$

    Integration by parts By repeatedly integrating by parts show that for $ n >1 $, $$ \int \frac{\ln^{n}(1-x)}{x} \ dx = \ln x \ln^{n}(1-x) + \sum_{k=1}^{n} (-1)^{k-1} \frac{n!}{(n-k)!} \text{Li}_{k+1}(1-x) \ln^{n-k} (1-x) + C$$ where $\text{Li}_{n}(x)$ is the polylogarithm function of order $n$.
Back
Top