What is Differentiation: Definition and 1000 Discussions

The cluster of differentiation (also known as cluster of designation or classification determinant and often abbreviated as CD) is a protocol used for the identification and investigation of cell surface molecules providing targets for immunophenotyping of cells. In terms of physiology, CD molecules can act in numerous ways, often acting as receptors or ligands important to the cell. A signal cascade is usually initiated, altering the behavior of the cell (see cell signaling). Some CD proteins do not play a role in cell signaling, but have other functions, such as cell adhesion. CD for humans is numbered up to 371 (as of 21 April 2016).

View More On Wikipedia.org
Recent contents Top users
  1. B

    Can you cancel a function out of a differential equation?

    I saw this in http://en.wikipedia.org/wiki/Momentum_operator From equation 4 to 5, it seems that a function is canceled out from the partial derivatives, is this possible?
  2. BiGyElLoWhAt

    Calculating Functional Derivatives: Understanding Notation and Examples

    If I understand what's going on (quite possibly I don't), I think my book is using bad (confusing) notation. Homework Statement As written: "Calculate ##\frac{\delta H[f]}{\delta f(z)} \ \text{where} \ H=\int G(x,y)f(y)dy##" and ##\frac{\delta H[f]}{\delta f(z)}## is the functional derivative...
  3. red1312

    How Do You Differentiate Complex Fractions in Calculus?

    Homework Statement Differentiate the following functions with respect to x Homework Equations (√2x-1)/ (lnx)? The Attempt at a Solution ln x (2x-10)^-1/2 -√(2x-1)(1/x)/(ln x)^2 ..........{This is a denominator} thank you [/B]
  4. K

    Solve for y(x) using the Fundamental Theorem of Calculus

    Homework Statement Solve the integral equation for y(x): y(x) = 1 + ∫ { [y(t)]^2 / (1 + t^2) } dt (integral from 0 to x) See attached image for the equation in a nicer format. Homework Equations Fundamental Theorem of Calculus The Attempt at a Solution dy/dx = y(x)^2 / (1 + x^2) ∫ dy/y^2 = ∫...
  5. B

    Differentiability in an open and closed intervals

    Is there an f(x) which is differentiable n times in a closed interval and (n+1) times in an open interval? I think I saw this in a paper related to Taylor's theorem (could be something else though). It didn't make sense to me, how can something be differentiable more in an interval that contains...
  6. binbagsss

    Meaning of tensor invariant, covariant differentiation

    E.g - considering co variant differentiation, The issue with the normal differentiation is it varies with coordinate system change. Covariant differentiation fixes this as it is in tensor form and so is invariant under coordinate transformations.'If a tensor is zero in one coordinate system...
  7. A

    Partial differentiation question rocket trajectory

    Homework Statement The problem and my attempt are attached Homework Equations Chain rule for partial differentiation perhaps And basic algebra The Attempt at a Solution I'm unsure of how to approach this but I differentiated all the expression at the top.
  8. P

    Deriving sec^3(x^3+csc^-1(cot^3\frac{x+4}{3x})) using chain rule

    Homework Statement hello i have to derive this equation ## sec^3(x^3+csc^-1(cot^3\frac{x+4}{3x})) ## 2. The attempt at a solution ##...
  9. AdityaDev

    How can \sqrt x and \log_e x be compared using calculus?

    I was going through some important points give in my textbook and I saw this: ##\log_e x < \sqrt x## How did they get this? I know calculus so you can show this using differentiation, etc. One possible way is that they took ##f(x)=\sqrt x-\log_e x## And tried to prove it is always greater than zero.
  10. T

    Isomorphism under differentiation

    Is 《sinx》under differentiation a valid cyclic group.
  11. I

    MHB Integration and Differentiation

    Evaluate ∫[sin2x/(1+(cos)^2 x) dx]Differentiate f(x) = (sin)^2 (e^((sin^2) x)) Hello, I'm just really stumped with these review questions and i have a test coming up. For the first, I'm not too sure what to do since there is a sin2x in general and for the second i don't know how to deal the...
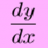
  12. iwantcalculus

    Trying to self-learn calculus but stuck on this idea

    So I started with limits and everything went well, and then into derivatives, and a problem started. First I know how to find the derivative of basic things using like ( limit definition of derivative) or (rules for derivatives) or ( product rule/ quotient rule/ chain rule)... My problem...
  13. M

    Differentiation of a sphere -- raindrop evaporating as it falls

    < Moderator Note -- Thread moved from the technical PF Calculus forum > I can't seem to grasp the idea of this problem, any help is much needed. The problem reads, "As a spherical raindrop falls, it reaches a layer of dry air and begins to evaporate at a rate that is proportional to its...
  14. M

    Differentiation of an exponential expression

    Homework Statement [/B] I need to differentiate the exponential function i = 12.5 (1-e^-t/CR) and I need to plot a table so that I can do a graph of i against t but I'm not sure how. (CR is the equivelant of Capacitance 20 Micro Fards and Resistance 300 Kilo Ohms)Homework Equations [/B] How do...
  15. F

    Partial Differentiation Question

    Homework Statement if z=\frac{1}{x^2+y^2-1} . Show that x \frac{\partial z}{\partial x} + y \frac{\partial z}{\partial y} = -2z(1+z) Homework Equations n/a The Attempt at a Solution I am extremely new to partial differentiation, I can get my head around questions where they just give...
  16. T

    Simple differentiation question

    Hey guys, Just a simple question to see if I'm going insane. So say I have an expression for: \frac{dxy}{dt} and an expression for \frac{dy}{dt} , how to I go about isolating an expression for just \frac{dx}{dt} I have tried using the product rule but it doesn't work for what I want. I know...
  17. M

    Differentiation of two similar systems

    Homework Statement Hi. i need help with understanding task with differentiation. i have two separate tasks, and i need help understanding why the solutions differ somewhat. system 1: Y = C + I + G C = f(Y-T) I = h(r) r = m(M) system 2: Y = C + I + G C = F(Y,T,r) I = f(Y,r) in system 1. when...
  18. K

    How Do I Apply Multivariable Calculus to Thermodynamics Problems?

    Homework Statement Homework Equations au/as=T au/av=p S/R=ln[(v-b)(u+a/c)^2] The Attempt at a Solution 1/T=1/au/as=as/au S=ln[(v-b)(U+a/v)^2]R as/au=[(v-b)2(U+a/v)(1)]R/[(v-b)(U+a/v)^2]=2R/(U+a/v)=1/T T=(U+a/v)/2R U=2RT-a/v au/av=-P au=-Pav integrate au to get u=-pv+c u=-pv+c=2RT-a/v...
  19. S

    Multi-variable Calculus : Partial differentiation

    Homework Statement 2. The attempt at a solution By chain rule, which simpifies to, After this I am struck.
  20. M

    MHB Reaction functions, differentiation question _ Game theory economics

    Consider a scenario where two individuals—Robert and Stuart—are under- taking a joint project, where the value generated from the project depends on the effort expended by both individuals. Let x be Robert’s level of effort and y the level of effort of Stuart; the value of the project for each...
  21. P

    How Should I Calculate dr² in Differentiation: Directly or by Finding dr First?

    In one physics problem if $$r^2= \lambda^2(1+\frac{m}{2\lambda})^2$$ what is ##dr^2 ?## Should I find ##dr## starting from ##r= \lambda(1+\frac{m}{2\lambda})## first and then square or find ##dr^2## starting from r^2? I know this is a basic question in differentiation using chain rule but it...
  22. F

    MHB Implicit differentiation difficult

    Given that $y'=\frac{tan(y)}{1-xsec^2(y)}$, find y'' in terms of $x$ and $y$ only. I've done this and checked my work several times but my answer does not agree with wolfram alpha. Sorry for not posting my work, I am a bit busy at the moment. Can someone show the first couple of lines of work...
  23. BiGyElLoWhAt

    Differentials? Can you elaborate?

    Disclaimer: This isn't a homework assignment, so maybe it shouldn't be in the homework forums. If you feel it should be located elsewhere, feel free to move it, but the template doesn't really apply to this question so... * * *...
  24. S

    Solve Differential Equation: dy/dx = dt

    hi, is it possible to solve the following equation, dy = dx/dt for relation between y and x? thanks
  25. N

    MHB Learn Implicit Differentiation: Solving for r^2 in $y^2 + x^2 = 0

    Can someone please explain how the result is obtained from the first line $r^2 = y^2 + x^2$ (refer to attached image)
  26. J

    Rademacher's Theorem: Introduction to Lipschitz Continuity

    Hello everyone, I was wondering if I could get a simple introduction to this Theorem since I will have to be giving a presentation on it within the next month. Based on the statement itself, there is an assumption made in the hypothesis which is something I haven't quite understood yet: If...
  27. A

    Why does differentiation find the approximate value?

    Like imagine I have to find the cube root of 8.03. So I cube 8 and use the dy=8+dy/dx*(8.03-8.00) formula. But why is this finding the value of cube root of 8.03 and why is this value approximate instead of exact?
  28. D

    Implicit differentiation; reproducing textbook derivation

    Homework Statement (The fourth equation is the central one) first, we have \frac{1}{r}=\frac{a}{b^2}(1+ecosθ) and b^2=a^2(1-e^2) now using these two, we transform acosψ=ae+rcosθ into (1-ecosψ)(1+ecosθ)=\frac{b^2}{a^2} we want to find dθ/dψ, and the author performs an inplicit...
  29. A

    Differentiation of Quotients and Higher Derivatives

    1) The line 2x+9=3 meets curve xy+y+2=0 at the points P and Q. Calculate the gradient of the curve at P and Q 2)Given that y=(x^2)/(x-2), find a) (d^2)y/dx^2 in its simplest form b)ther range of value for which dy/dx and (d^2)y/dx^2 are positive. I can't figure out either of the sums...
  30. S

    Deriving the Angular Momentum of a Particle: Proof of Differentiation

    Homework Statement Angular momentum of a particle is: L = (dr/dt) x mr Show that (dL/dt) = (d2r/dt2) x mr Homework Equations ----- The Attempt at a Solution My atempt is that I tried writing it in the form y = mx + c but I don't think that would be relevant. Next I tried...
  31. EverGreen1231

    Question on the differentiation between a Network line from Radial

    I have been told that if the line connects breaker to breaker, it is considered to be radial; but, this doesn't make sense to me. If a line is connected by two feeders then there would be two sources of power, hence "Radial". I'm not sure if I'm missing some minute detail that makes the whole...
  32. F

    MHB Question about implicit differentiation

    Say you want to find the slop of a tangent line of the circle x^2+y^2=25 I was following the directions here. I don't completely understand how the derivative of y^2 becomes 2y\frac{dy}{dx}. Shouldn't it become 0 if we are taking the derivative with respect to x? The website explains but to me...
  33. B

    Differentiation in Minkowski Spacetime

    Hello everybody, I'm currently reading the book Special Relativity in General Frames by Gourgoulhon. There, Minkowski Spacetime is introduced as an affine space \mathscr{E} over \mathbb{R} with a bilinear form g on the underlying vector space E that is symmetric, nondegenerate an has signature...
  34. M

    MHB Solving an integral using Differentiation under the integral sign

    I am Trying to solve the difference of the two following integrals: (1) $g_{1}(x) = \int_{0}^{\infty} \frac{cos(kx)}{k}\,dk$ (2) $g_{2}(x) = \int_{0}^{\infty} \frac{\exp(-2k)cos(kx)}{k}\,dk$ I read the thread on Advanced Integration Techniques and it...
  35. T

    Differentiation of conic section equation

    Homework Statement I do not understand how the authors got the time derivative of equation 1.5-4 in the form given at 2.5-2. Homework Equations The Attempt at a Solution \frac{d}{dt}\frac{p}{1+e...
  36. C

    Differentiation of a Taylor series

    Homework Statement Hi guys, any help on this question would be hugely appreciated. The Taylor series about 0 for the function f(x)=(1/4+x)-3/2 is f(x)=8 - 48x + 240x^2 - 1120x^3 + ... used differentiation to find the Taylor series about 0 for the function g(x)=(1/4+x)-5/2 The...
  37. J

    Logarithm differentiation + chain rule

    For this function y=\sqrt{2ln(x)+1} if I use the chain rule properly, should I be getting this answer? \frac{dy}{dx}=\frac{2}{x} \times \frac{1}{2} \times \frac{1}{\sqrt{2ln(x)+1}} My aim of doing this is to verify that \frac{dy}{dx}=\frac{1}{xy}
  38. J

    Differentiation between massless Bosons

    Three Bosons: the Photon, the Gluon, and the Graviton are all massless Bosons; they all travel at the speed of light and therefore have no interaction with the Higgs field. How is it possible to differentiate between these three particles being that the Photon is a Majorana Fermion and therefore...
  39. A

    MHB Differentiation With L'Hopital's Rule

    Hey guys, Need some more help again. I'll keep it brief. This thread is only for question 2ab. Please ignore question 1: For 2a, I simply employed L'Hopital's Rule since 0/0 is indeterminate form. Thus, my final answer came out to be: ln6-ln3. As for 2b, I computed an indeterminate form...
  40. A

    MHB Logarithmic Differentiation And Exponential Growth Questions

    Hey guys, I have a couple more questions about this problem set I've been working on. I'm doubting some of my answers and I'd appreciate some help. Question: For the first one (part a), I went through the steps for logarithmic differentiation by using the ln laws to separate terms, and then...
  41. A

    MHB Differentiation Techniques in Calculus

    Hey guys, I have a couple of questions about this problem set I've been working on. I'm doubting some of my answers and I'd appreciate some help. Question: For 1a, I just separated the function into single terms with √x as the denominator. This ultimately resulted in: (5/2)x^(3/2) - (9/2)√x +...
  42. Greg Bernhardt

    What is implicit differentiation

    Definition/Summary The definition of a function y of x is explicit if it is an equation in which y appears only once, and on its own (usually by starting "y ="). In any other case, the definition of a function y of x is implicit. Implicit differentiation of y with respect to x is a...
  43. Mr-R

    Covariant differentiation twice

    Doing some problems in D'INVERNO GR textbook and I am stuck on taking the covariant derivation of a tensor twice. Please see the attached picture and please do inform me if something is not clear :smile:
  44. V

    Abstractions of integration and differentiation

    I have a few questions about the generalizations of concepts like integration and differentiation of single-valued functions of a single variable to vector-valued functions of several variables. All in the context of real analysis. Beginning with scalar-valued functions of several variables...
  45. ryanuser

    Why is the differentiated 2x 2 but not x squared?

    I apologise because my question is more mathematically related than physical, however I was unsuccessful at finding a better place to ask. My question is how the differentiated 2x is 2 but not x squared? I learned that In order to differentiated, we place the number that x has been powered to...
  46. G

    Chain Rule Differentiation: Simplifying Trigonometric Expressions

    The question: This is the solution that was given by my teacher Attempt: I understand how the work is done until the 3-4 line. Where did the 1-cos2x disappear to in the 4th line? I know you can use the outside inside method but try as I might, I can't seem to understand how the final...
  47. DreamWeaver

    MHB A curvature problem (differentiation)

    In the Euclidean plane, assume a differentiable function y=f(x) exists. At any given point, say (x_0,y_0), the line tangential to y=f(x) at this point intersects the x-axis at an angle \phi. The curvature of this curve, \kappa, is the rate of change of \phi with respect to arc length, s...
  48. DreamWeaver

    MHB An almost elementary differentiation problem....

    Let \zeta(x) be the Zeta function (where, for convenience, x is assumed to be > 1). \zeta(x) = \sum_{k=1}^{\infty}\frac{1}{k^x}Similarly, define the Eta function (alternating Zeta function) by the following series - where again, in this case, we assume x > 1:\eta(x) =...
  49. DreamWeaver

    MHB How are the Hermite Polynomials Defined and Calculated?

    Defining the Hermite Polynomials by: \mathscr{H}_n(x) = (-1)^n e^{x^2}\, \frac{d^n}{dx^n} \Bigg\{ e^{-x^2}\Bigg\}Show that \mathscr{H}_5(x) = 32 x^5-160 x^3+120 x
  50. T

    Tensor differentiation (element-by-element)

    Homework Statement Proof the following: \frac{\text{d}\boldsymbol\{\mathbf{I}\boldsymbol\}}{\text{d}t} \, \boldsymbol\omega = \boldsymbol\omega \times (\boldsymbol\{\mathbf{I}\boldsymbol\}\,\boldsymbol\omega) where \boldsymbol\{\mathbf{I}\boldsymbol\} is a tensor...
Back
Top