What is Integration: Definition and 1000 Discussions

System integration is defined in engineering as the process of bringing together the component sub-systems into one system (an aggregation of subsystems cooperating so that the system is able to deliver the overarching functionality) and ensuring that the subsystems function together as a system, and in information technology as the process of linking together different computing systems and software applications physically or functionally, to act as a coordinated whole.
The system integrator integrates discrete systems utilizing a variety of techniques such as computer networking, enterprise application integration, business process management or manual programming.System integration involves integrating existing, often disparate systems in such a way "that focuses on increasing value to the customer" (e.g., improved product quality and performance) while at the same time providing value to the company (e.g., reducing operational costs and improving response time). In the modern world connected by Internet, the role of system integration engineers is important: more and more systems are designed to connect, both within the system under construction and to systems that are already deployed.

View More On Wikipedia.org
Recent contents Top users
  1. kupid

    MHB Calculus & Diff. Eqn: Beginner Qs on Function, Derivative & Gradient

    I have some beginner doubts about Calculus and Differential equations . Is a function always a curve ? Doesn't a function already has a slope ? d/dx of a function gives the gradient of the curve between two points ? The derivative ,d/dx ,The gradient , is the rate of change of a...
  2. J

    A Analytical Integration of a Difficult Function

    Is it possible to integrate the following function analytically? ##\int_{0}^{\infty} \frac{\exp{-(\frac{A}{\tau}+B\tau+\frac{A}{\beta-\tau})}}{\sqrt{\tau(\beta-\tau)}}d\tau,## where ##A##, ##B## and ##\beta## are real numbers. What sort of coordinate transformation makes the integral bounded...
  3. S

    Integration with hyperbolic secant

    Homework Statement Solve ##\displaystyle{d\sigma = \frac{d\rho}{\cosh\rho}.}## Homework Equations The Attempt at a Solution The answer is ##\displaystyle{\sigma = 2 \tan^{-1}\text{sinh}(\rho/2)}##. See equation (10.2) in page 102 of the lecture notes in...
  4. Sarah00

    Integration. Where is the mistake? (if there is)

    Homework Statement Homework EquationsThe Attempt at a Solution My Solution: My Friend Solution: Are we both right? If not, who is right? and what is the mistake in other's solution! Thanks![/B]
  5. M

    I Find total charge (using double integration)

    The question asks to find total charge in a region given x has lower bound 0 - upper bound 5 , y has lower bound as 2 and upper bound as 5. Based on knowledge I have been reading throughout the chapter, I set up a double integration with those dxdy, but the results went out to be off - compared...
  6. binbagsss

    I Does dP_x dP_y = d^2\vec P : Integration scalar / vector var

    Excuse me if this is a bad question but: Does ##d P_x d P_y = d^2 \vec P ##? I thought not because ##P_x ## is a scalar , a component of the vector, whereas ##\vec P ## is a vector? Thanks in advance
  7. F

    I Integral involving square and log

    I have this integral that when solved, involves squares and natural logs, where ##A\,##,##\,b\,##, and ##\,x_e\,## are constants while ##x## is a variable. ##A = \int_{x_e}^{x} \frac{x^2 - b^2}{x} dx = \int_{x_e}^{x} x \, dx -b^2 \int_{x_e}^{x} \frac{dx}{x} = \frac{x^2}{2} - \frac{x_e^2}{2} -...
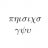
  8. davidge

    I Integrals: Why Change from M to $\phi(M)$?

    Yes, I know that I have already created another thread on this subject before. But, in this one, I would like to ask specifically why should we change from ##M## to ##\phi (M)## in the integral below? $$ \int_M (\partial_\nu w_\mu - \partial_\mu w_\nu) \ dx^\nu \wedge dx^\mu = \int_{\phi (M)}...
  9. X

    I Integration over something with addition in denominator

    Hi, I'm struggling to figure out how to do integration with forms such as: ∫ x/(x+1) dx ∫ x/(x+1)^2 dx ∫(b-x)^2/(b-a) dx This last one especially is giving me a strange issue, where if I plug it into wolfram: https://www.wolframalpha.com/input/?i=integrate+(b+-+x)%5E2+%2F(b-a)++dx It shows...
  10. D

    Integration of Thermodynamics equation w=–∫vDP

    Homework Statement Integrate w=–∫vDP from 2 to 1 and get k(P2V2-P1V1/1-k) The equation is used for steady flow, reversible and Ideal gas Homework EquationsThe Attempt at a Solution I'm not sure how to get the result
  11. doktorwho

    How to Prove the Integral Property for Definite Integrals

    Homework Statement Today i had a test on definite integrals which i failed. The test paper was given to us so we can practise at home and prepare better for the next one. This is the first problem which i need your help in solving:: Homework Equations 3. The Attempt at a Solution [/B] As no...
  12. B

    Calculus Books to learn integration techniques ?

    Are there books that are solely devoted to solving integrals and different methods in solving them ? I like solving integrals and I want to learn different techniques to solve integrals.
  13. binbagsss

    Cts approximation, delta function integration, stat mech

    Homework Statement Homework EquationsThe Attempt at a Solution So cts approx holds because ##\frac{E}{\bar{h}\omega}>>1## So ##\sum\limits^{\infty}_{n=0}\delta(E-(n+1/2)\bar{h} \omega) \approx \int\limits^{\infty}_{0} dx \delta(E-(x+1/2)\bar{h}\omega) ## Now if I do a substitution...
  14. Helmholtzerton

    MATLAB Filter out constant of integration?

    Hello, I'm trying to integrate a signal received on an oscilliscope, but I'm afraid using the function cumtrapz is not giving me the correct value. Here is what I'm seeing when testing out sine functions I could apply an FFt to obtain the components and the phases, and then subtract off the...
  15. F

    Complex integration on a given path

    Homework Statement Calculate the following integrals on the given paths. Why does the choice of path change/not change each of the results? (a) f(z) = exp(z) on i. the upper half of the unit circle. ii. the line segment from − 1 to 1. Homework Equations ∫γf(z) = ∫f(γ(t))γ'(t)dt, with the...
  16. P

    Verify orthogonality integral by direct integration

    This is a heat equation related math problem. 1. Homework Statement The complete question is: Verify the orthogonality integral by direct integration. It will be necessary to use the equation that defines the λ_n: κ*λ_n*cos(λ_n*a) + h*sin(λ_n*a)=0. Homework Equations κ*λ_n*cos(λ_n*a) +...
  17. S

    Density & Integration.... Help?

    Homework Statement A hole in the ground in the shape of an inverted cone is 19 meters deep and has radius at the top of 16 meters. The cone is filled to the top with sawdust. The density of the sawdust depends upon the depth, x, following the formula ρ(x) = 2.1 + 1.2e^(-1.2x) kg/m^3. Find the...
  18. Macykc2

    Can I Use Antiderivatives to Evaluate this Complex Integral?

    Homework Statement I need to evaluate the following integral using the antiderivative: $$\int log^2(z) \, dz$$ I don't know how to make a subscript for the integral sign, there should be a "c" on the bottom part. C is any contour from ##π## to ##i##, not crossing the non-positive x-axis...
  19. Unteroffizier

    How is gravitational acceleration affected with distance?

    Note: I didn't really know where to put this. It isn't a specific problem, but I've been asked by my physics teacher, who decided to give me and a few others an individual physics course of sorts, to find the means of solving similar problems. It's the first problem he assigned us, since we're...
  20. H

    Explanation for integration of Dr/Dt

    Homework Statement Why integration of $$\frac{D^2\mathbf r}{Dt^2}=−2\mathbf w \times \frac{D\mathbf r}{Dt}−g\mathbf R$$ gives us $$\frac{D\mathbf r}{Dt}= \mathbf v_0 −2\mathbf w×(\mathbf r−\mathbf r_0)−gt\mathbf R$$ Homework Equations Consider a time-varying vector written in the body...
  21. C

    I Limits of integration on Polar curves

    General question, how do you determine the limits of integration of a polar curve? Always found this somewhat confusing and can't seem to find a decent explanation on the internet.
  22. K

    B Applying L'Hospital's rule to Integration as the limit of a sum

    The definite integral of a function ##f(x)## from ##a## to ##b## as the limit of a sum is: $$\int_a^bf(x)dx=\lim_{h\rightarrow 0}h(f(a)+f(a+h)+.. ..+f(a+(n-2)h)+f(a+(n-1)h))$$ where ##h=\frac{b-a}{n}##. So, replacing ##h## with ##\frac{b-a}{n}## gives: $$\lim_{n\rightarrow...
  23. karush

    MHB Integration By Parts: uv-Substitution - 9.2

    $\tiny{9.2}$ \begin{align*} \displaystyle I&=\int y^3e^{-9y} \, dx\\ \textit{uv substitution}\\ u&=y^3\therefore \frac{1}{3}du=y^2dx\\ dv&=e^{-9y}\, dx\therefore v=e^{-9y}\\ \end{align*} will stop there this looks like tabular method better
  24. Demystifier

    I Error in Lorentz Invariant Integration

    Let ##j^{\mu}(x)## be a Lorentz 4-vector field in Minkowski spacetime and let ##\Sigma## be a 3-dimensional spacelike hypersurface with constant time of some Lorentz frame. From those I can construct the quantity $$Q=\int_{\Sigma} dS_{\mu}j^{\mu}$$ where $$dS_{\mu}=d^3x n_{\mu}$$ and ##n_{\mu}##...
  25. mercenarycor

    Contour integration with a branch cut

    Homework Statement ∫-11 dx/(√(1-x2)(a+bx)) a>b>0 Homework Equations f(z0)=(1/2πi)∫f(z)dz/(z-z0) The Attempt at a Solution I have absolutely no idea what I'm doing. I'm taking Mathematical Methods, and this chapter is making absolutely no sense to me. I understand enough to tell I'm supposed...
  26. Conductivity

    B Integration by Substitution Using Infinite Sums

    I have seen the wikipedia's proof which can be found here: https://proofwiki.org/wiki/Integration_by_Substitution However sometimes, we have problems where you have a ##d(x)## times ## f(g(x))## times g prime of x where we use substitution and it works but the proof didn't prove this...
  27. doktorwho

    Integration by substitution question

    Homework Statement Question: To solve the integral ##\int \frac{1}{\sqrt{x^2-4}} \,dx## on an interval ##I=(2,+\infty)##, can we use the substitution ##x=\operatorname {arcsint}##? Explain Homework Equations 3. The Attempt at a Solution [/B] This is my reasoning, the function ##\operatorname...
  28. K

    B Is the theory of fractional-ordered calculus flawed?

    Let's talk about the function ##f(x)=x^n##. It's derivative of ##k^{th}## order can be expressed by the formula: $$\frac{d^k}{dx^k}=\frac{n!}{(n-k)!}x^{n-k}$$ Similarly, the ##k^{th}## integral (integral operator applied ##k## times) can be expressed as: $$\frac{n!}{(n+k)!}x^{n+k}$$ According...
  29. E

    I Question about integration in physics

    I've always thought of integration as a way to solve differential questions. I'd solve physics problems involving calculus by finding the change in the function df(x) when I increment the independent variable (say x of f(x)) by an infinitesimal amount dx, attaching some physical significance to...
  30. K

    B Average angle made by a curve with the ##x-axis##

    The average angle made by a curve ##f(x)## between ##x=a## and ##x=b## is: $$\alpha=\frac{\int_a^b\tan^{-1}{(f'(x))}}{b-a}$$ I don't think there should be any questions on that. Since ##f'(x)## is the value of ##\tan{\theta}## at every point, so ##tan^{-1}{(f'(x))}##, should be the angle made by...
  31. EthanVandals

    Integration by Parts Twice: How to Solve Tricky Integrals

    Homework Statement Integrate e^3x sin x. Homework Equations uv - Integral(v du) The Attempt at a Solution I am trying to help somebody else with this problem, as I took Calculus a few years ago, but the end is really kicking my butt. I know I'm VERY close, but once I get to the second...
  32. Jovy

    Integrate $$y= \frac 1 {\sqrt{2\pi}}e^{ \frac{- x^2} 2},~y=0,~x=0,~x=1$$

    Homework Statement [/B] $$y= \frac 1 {\sqrt{2\pi}}e^{ \frac{- x^2} 2},~y=0,~x=0,~x=1$$ Homework Equations $$Volume=2\pi\int_a^b p(x)h(x)dx$$ The Attempt at a Solution I understand how to do the problem, I'm just having trouble integrating. ##h(x)=\frac 1 {\sqrt{2\pi}}e^{ \frac{- x^2} 2},~...
  33. E

    Why is the integral of a(x) different from the integral of a(t)?

    Hello! First time poster, please treat me well! :wink: I've already solved the problem below on my second attempt with the help of kinetic energy but I want to know why my first attempt gives a wrong answer. 1. Homework Statement A force in the +x-direction with magnitude F(x) = 18.0 N -...
  34. M

    I Clarification about Integration

    Hello, I am new to the forum and need some help understanding how to evaluate this integral symbolically. ∫∫ r dA The differential element lies within a circle that is offset from the y-axis by some value R2, and the radius of the circle is R1. Again, the circle center location is (0,R2)...
  35. M

    Understanding Integration Limits for Spherical and Cartesian Coordinates

    Homework Statement Shown in the photo attached. 2. Homework Equations ∫V r2Sinθdθdφdr in spherical coordinates ∫V dxdydz in cartesian coordinates equation of a sphere x2+y2+z2=r2 The Attempt at a Solution In this case y=(y-2): sphere displaced on the y-axis. and since it is bound by all...
  36. F

    I Deformation of contour of integration or shifting poles

    As I understand it, in order to compute a contour integral one can deform the contour of integration, such that it doesn't pass through any poles of the integrand, and the result is identical to that found using the original contour of integration considered. However, I have seen applications...
  37. Dopplershift

    Limits of Integration of a Triangle

    Homework Statement Suppose you have a Triangle with the vertices, (0,0) (1,1) and (0,1). Integrating along that path. I have some differential function dZ where Z = Z(x,y) Homework EquationsThe Attempt at a Solution [/B] If I need to integrate, then I need to find the limits of...
  38. S

    I Solve Nonlinear DE: Friedmann Eqns for H 0-10^7

    From cosmology, the friedmann equations are given by, ##H^2 = (\frac{\dot a}{a})^2 = \frac{8\pi G}{3} \rho \, , \quad \frac{\ddot a}{a} = -\frac{4\pi G}{3}(\rho+3p) \, , \quad## where ##\rho = \frac{1}{2}(\dot \phi^2 + \phi^2)## and ##p = \frac{1}{2}(\dot \phi^2 - \phi^2)## To get ##\dot H##...
  39. Kurd

    Double integration problem for IDSFT

    Homework Statement [/B] The 2D Discrete Space Fourier transform (DSFT) X(w1,w2) of the sequence x(n1,n2) is given by, $$X(w_1,w_2) = 5 + 2j sin(w_2) + cos(w_1) + 2e^{(-jw1-jw2)}$$ determine x(n1,n2)Homework Equations By definition inverse DSFT is, $$x(n_1,n_2) = \dfrac{1}{(2π)^2}...
  40. Duke Le

    Where is wrong in this proof for rotational inertia ?

    Homework Statement Prove the formula for inertia of a ring (2D circle) about its central axis. Homework Equations I = MR^2 Where: M: total mass of the ring R: radius of the ring The Attempt at a Solution - So I need to prove the formula above. - First, I divide the ring into 4...
  41. chwala

    Solve Integration Problem: tan θ sec θ → (1/2)ln(3/2)

    Homework Statement given ## tan 2θ-tan θ≡ tan θ sec 2θ## show that ##∫ tan θ sec θ dθ = (1/2 )ln (3/2)## limits are from θ= 0 to θ=π/6 Homework EquationsThe Attempt at a Solution ##∫ tan 2θ-tan θ dθ ## → -(1/2 )ln cos 2θ + ln cos θ → ##-1/2 ln 1/2 + ln √3/2## ##= ln (√3)/2-...
  42. chwala

    Integration problem using substitution

    Homework Statement using ## u= sin 4x## find the exact value of ##∫ (cos^3 4x) dx##[/B]Homework EquationsThe Attempt at a Solution ## u= sin 4x## [/B]on integration ##u^2/2=-cos4x/4 ## , →##-2u^6={cos 4x}^3 ##...am i on the right track because now i end up with...
  43. Angelo Cirino

    I Laplacian in integration by parts in Jackson

    I am reviewing Jackson's "Classical Electromagnetism" and it seems that I need to review vector calculus too. In section 1.11 the equation ##W=-\frac{\epsilon_0}{2}\int \Phi\mathbf \nabla^2\Phi d^3x## through an integration by parts leads to equation 1.54 ##W=\frac{\epsilon_0}{2}\int |\mathbf...
  44. yecko

    Simple integration for an area problem

    Homework Statement Homework Equations Integration of graph is the area. The Attempt at a Solution I don't think my way should have any problem in it, but I can't get the right answer. Are there any careless mistakes in it? Or any other problems? And how is the true answer get? And what is...
  45. jlmccart03

    Show Wolfram Alpha's answer is equivalent to my answer.

    Homework Statement Integrate x2(2+x3)4dx. Show that Wolfram Alpha's answer is equivalent to your answer. Homework Equations No equations besides knowing that the integral of xpower is 1/power+1 * xpower + 1 The Attempt at a Solution So I have the answer to the integral by hand as (2+x3)5)/15...
  46. O

    I Epsilon-delta vs. infinitesimal

    Background: mechanical engineer with a flawed math education (and trying to make up for it). I have recently read this statement (and others like it): "We shall also informally use terminology such as "infinitesimal" in order to avoid having to discuss the (routine) "epsilon-delta" analytical...
  47. T

    Integrating with respect to area? Past paper question

    This isn't exactly homework or coursework, it is a past paper question that I cannot find a solution to (my university doesn't like releasing answers for some reason unknown to me). The question is attached as an image (edit: the image displays while editing but not in the post, so I'll try to...
  48. J

    Why Does Trig Substitution Yield Different Integral Results?

    Homework Statement ∫8cos^3(2θ)sin(2θ)dθ Homework EquationsThe Attempt at a Solution rewrote the integral as: 8∫(1-sin^2(2θ))sin(2θ)cos(2θ)dθ u substitution with u=sin(2θ) du=2cos(2θ)dθ 4∫(1-u^2)u du= 4∫u-u^3 du 4(u^2/2-u^4/4)+C undo substitution and simplify 2sin^2(2θ)-sin^4(2θ)+C The book...
  49. J

    How Is Rocket Speed and Height Calculated Under Varying Thrust and Mass?

    Homework Statement A rocket with initial mass of m0. The engine that can burn gas at a rate defined by m(t)=m0-αt, and expel gas at speed (relative to the rocket) of u(t)=u0-βt. Here, m0, α, u0, and β are all constants. Assume the lift-off from ground is immediate a) The rocket speed v(t)=...
  50. M

    Determine the surface of a cardioid

    Homework Statement Consider the cardioid given by the equations: ##x = a(2\cos{t} - \cos{2t})## ##y = a(2\sin{t} - \sin{2t})## I have to find the surface that the cardioid circumscribes, however, I don't know what limits for ##t## I have to take to integrate over. How can I know that, as I...
Back
Top