You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
What is Curve: Definition and 1000 Discussions
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight.
Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that appeared more than 2000 years ago in Euclid's Elements: "The [curved] line is […] the first species of quantity, which has only one dimension, namely length, without any width nor depth, and is nothing else than the flow or run of the point which […] will leave from its imaginary moving some vestige in length, exempt of any width."This definition of a curve has been formalized in modern mathematics as: A curve is the image of an interval to a topological space by a continuous function. In some contexts, the function that defines the curve is called a parametrization, and the curve is a parametric curve. In this article, these curves are sometimes called topological curves to distinguish them from more constrained curves such as differentiable curves. This definition encompasses most curves that are studied in mathematics; notable exceptions are level curves (which are unions of curves and isolated points), and algebraic curves (see below). Level curves and algebraic curves are sometimes called implicit curves, since they are generally defined by implicit equations.
Nevertheless, the class of topological curves is very broad, and contains some curves that do not look as one may expect for a curve, or even cannot be drawn. This is the case of space-filling curves and fractal curves. For ensuring more regularity, the function that defines a curve is often supposed to be differentiable, and the curve is then said to be a differentiable curve.
A plane algebraic curve is the zero set of a polynomial in two indeterminates. More generally, an algebraic curve is the zero set of a finite set of polynomials, which satisfies the further condition of being an algebraic variety of dimension one. If the coefficients of the polynomials belong to a field k, the curve is said to be defined over k. In the common case of a real algebraic curve, where k is the field of real numbers, an algebraic curve is a finite union of topological curves. When complex zeros are considered, one has a complex algebraic curve, which, from the topological point of view, is not a curve, but a surface, and is often called a Riemann surface. Although not being curves in the common sense, algebraic curves defined over other fields have been widely studied. In particular, algebraic curves over a finite field are widely used in modern cryptography.
View More On Wikipedia.org
Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that appeared more than 2000 years ago in Euclid's Elements: "The [curved] line is […] the first species of quantity, which has only one dimension, namely length, without any width nor depth, and is nothing else than the flow or run of the point which […] will leave from its imaginary moving some vestige in length, exempt of any width."This definition of a curve has been formalized in modern mathematics as: A curve is the image of an interval to a topological space by a continuous function. In some contexts, the function that defines the curve is called a parametrization, and the curve is a parametric curve. In this article, these curves are sometimes called topological curves to distinguish them from more constrained curves such as differentiable curves. This definition encompasses most curves that are studied in mathematics; notable exceptions are level curves (which are unions of curves and isolated points), and algebraic curves (see below). Level curves and algebraic curves are sometimes called implicit curves, since they are generally defined by implicit equations.
Nevertheless, the class of topological curves is very broad, and contains some curves that do not look as one may expect for a curve, or even cannot be drawn. This is the case of space-filling curves and fractal curves. For ensuring more regularity, the function that defines a curve is often supposed to be differentiable, and the curve is then said to be a differentiable curve.
A plane algebraic curve is the zero set of a polynomial in two indeterminates. More generally, an algebraic curve is the zero set of a finite set of polynomials, which satisfies the further condition of being an algebraic variety of dimension one. If the coefficients of the polynomials belong to a field k, the curve is said to be defined over k. In the common case of a real algebraic curve, where k is the field of real numbers, an algebraic curve is a finite union of topological curves. When complex zeros are considered, one has a complex algebraic curve, which, from the topological point of view, is not a curve, but a surface, and is often called a Riemann surface. Although not being curves in the common sense, algebraic curves defined over other fields have been widely studied. In particular, algebraic curves over a finite field are widely used in modern cryptography.
View More On Wikipedia.org
-
T
Finding a Piecewise Smooth Parametric Curve for the Astroid
Homework Statement Find a piecewise smooth parametric curve to the astroid. The astroid, given by $\phi(\theta) = (cos^3(\theta),sin^3(\theta))$, is not smooth, as we see singular points at 0, pi/2, 3pi/2, and 2pi. However is there a piecewise smooth curve? Homework Equations $\phi(\theta) =...- ttsp
- Thread
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-

6 dB of IF response curve....?
Hi folks, My query is that... As one can see that in the IF response curve the picture carrier is placed 6db down the amplitude curve. Such a placement modifies the output of video detector in such a way that the picture carrier lies at half point or 50 % of the total amplitude. Now this whole...- brainbaby
- Thread
- Replies: 16
- Forum: Electrical Engineering
-

What is the fastest speed around a curve?
I understand that the centripetal force on an object of mass 'm' is (mv2)/r However, isn't this for an object going around in a circle? Suppose I have a curve (0.0033x2+−1.0038x+98.2331). What would be the fastest speed around this curve on the bounds x -> Please note that we would...- Natus Homonymus
- Thread
- Replies: 10
- Forum: Mechanics
-

Null curve coordinate system
So, I've been studying some tensor calculus for general theory of relativity, and I was reading d'Inverno's book, so out of all exercises in this area(which I all solved), this 6.30. exercise is causing quite some problems, so far. Moreover, I couldn't find anything relevant on the internet that...- Antarres
- Thread
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-

A man is driving around a curve rather quickly one day
Homework Statement a man is driving around a curve rather quickly one day at 21.2m/s. He has an object hanging from his mirror that makes an angle of 36.4 wih respect to vertical as he goes around the curve. What is the radius of the curve? Homework EquationsThe Attempt at a Solution I set up...- HappyFlower
- Thread
-
- Tags
- Curve
- Replies: 5
- Forum: Introductory Physics Homework Help
-

Length of the curve - parametric
Homework Statement [/B] Find the definite integral formula for the length of the curve for $$0 \leq t \leq \frac \pi 2$$ $$x = 2*cos^k(t)$$ $$y = 2*sin^k(t)$$ for general $$k \gt 0$$2. The attempt at a solution I don't understand why this is wrong: $$\int_0^\frac \pi 2\...- Poetria
- Thread
-
- Tags
- Curve Length Parametric
- Replies: 7
- Forum: Calculus and Beyond Homework Help
-
Z
Finding the Torque vs RPM curve for a 3-phase AC induction motor
Dear community, For one of the projects which I am currently working on, I want to quantify my three phase AC induction motor in the following ways: 1. Find Torque vs RPM Curve 2.Find Efficiency vs RPM Curve Now since I don't have the industrial "Torque Sensor" to plot Torque vs RPM curves, I...- zaraf
- Thread
- Replies: 4
- Forum: Electrical Engineering
-
F
Point on the curve closest to (18,1)
Question: Question: Find the point on the curve y=x^2 +1 that is closest to the point (18,1). Please see the image and that’s where I’m stucked- after taking the first derivate. Please solve it further step by step completely. It’d mean a lot.- Faraz Ahmed
- Thread
-
- Tags
- Curve Differentiation Point
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
P
Calculating curve for a machine
Mod note: Thread moved from the Precalc Homework section 1. Homework Statement So I am designing a machine. the issue is I have to calculate like 8 things and the maths is floating in my head but I can't get there. the requirements are that X axis squared + Y axis Squared = 75 Squared. then...- Phillip81
- Thread
- Replies: 5
- Forum: Mechanical Engineering
-

What is the shape of the curve z = x^2 + 2y^2 and how can it be sketched?
Homework Statement [/B] Sketch the curve z = x2 + 2y2Homework Equations None[/B]The Attempt at a Solution : [/B]The easiest thing to do is to sketch the traces at x, y and z = 0. I'm 95% sure its an elliptic paraboloid, but the 2 in front of the Y is really throwing me off. Should we...- tensor0910
- Thread
-
- Tags
- Curve
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
H
What is the Method for Finding Area Between Curves?
Homework Statement Homework Equations The Attempt at a Solution I'm confused avout questions 2-3. The answers for 2-2 is 1 So the answer for 2-3 is $$\frac{1}{3}$$ But, how the area looks like? Because $$ x^2 $$ will be an open curve upside? There's no boundary for above side. -
R
I Rate of change of area under curve f(x) = f(x)
What lead to the equality of the, rate of change of area under curve f(x) = f(x). Was it, they were just compared(OR believed to be equal) and mathematically found to be equal. Or when one was integrated or differentiated the other appeared. Also I knew, integration was being used since...- rajeshmarndi
- Thread
- Replies: 3
- Forum: Calculus
-
J
Defining Multi-Linear Isotropic Stress-Strain Curve Ansys WB
In order to use Solid65 in Ansys workbench for simulating concrete, we shall define the multi-linear isotropic stress-strain curve as well. I have the concrete compression stress-strain data in excel. I would like to ask that how could I get the multi-linear isotropic stress-strain curve in...- jackhero
- Thread
- Replies: 1
- Forum: General Engineering
-

What is the line integral of a curve?
Homework Statement Homework EquationsThe Attempt at a Solution Line integral of a curve ## I = \int_{ }^{ } yz dx + \int_{ }^{ } zx dy + \int_{ }^{ } xy dz ## with proper limits. ## I = \int_{\frac { \pi }4}^{ \frac { 3 \pi} 4} abc ( \cos^2 t - \sin^2 t ) dt = -abc ## |I| = abc...- Pushoam
- Thread
- Replies: 12
- Forum: Calculus and Beyond Homework Help
-

MHB What is the length of a curve defined by a logarithmic function?
$\begin{align*}\displaystyle f(x)&=\ln(\sin{x})\\ \frac{\pi}{6}& \le x \le \frac{\pi}{2}\\ \end{align*}$ $\begin{align*}\displaystyle f^\prime(x)&=\cot{x} \end{align*}$ so $\begin{align*}\displaystyle L&=\int_{\pi/6}^{\pi/2} \sqrt{1- (\cot{x})^2} \,dx \\ \therefore... -
K
Graph drawing—Finding the points on a curve that are nearest to the origin
Homework Statement Homework Equations First derivative=maxima/minima/vertical tangent/rising/falling When f'(x)>0 ? the function rises The Attempt at a Solution Deriving relative to x: $$10x-6(yy'+x)+10yy'=0~\rightarrow~y'=-\frac{x}{y}$$ What do i do with that? -
T
MHB Area between the curve and x axis
Hey guys, I've got this question in my book, and I think that I may be misunderstanding the concept. The book is somewhat lacking on this particular question, and has left me in the dark to some degree. The question is Find the area between the curve y=2/(x-1)dx and the x-axis over the...- TheFallen018
- Thread
- Replies: 8
- Forum: Calculus
-

Find the Coefficient of friction on a banked curve.
Homework Statement A car giving a turn on a curve with 88m of radius, traveling at a speed of 95km/h, the curve is perfectly banked for a car traveling at 75 km/h, meaning that the curve has an angle θ of 26.7º. Homework Equations μ = ? r = 88m v = 26.38 m/s θ = 26.7º Ff = μ · g · m Fc = m...- Motzu2098
- Thread
- Replies: 9
- Forum: Introductory Physics Homework Help
-
M
MHB Calculate directly the curve integrals
Hey! :o We consider the space $D$ that we get if we remove from the square $[-2,7]\times [-3,6]$ the open discs with center the point $(0,0)$ and radius $1$ and with center $(3,3)$ and radius $2$. I want to calculate $$\sum_{j=1}^3\oint_{\sigma_j}\left... -

GR: find covariantly constant vector on a given curve
Homework Statement I am stuck on finding ##W^u## Homework Equations [/B] I have computed the christoffel symbols via comparing the Euler-Lagrange equations to the form expected from geodesic equation. geodesic equation: ##\ddot{x^a}+\Gamma^a_{bc}\dot{x^b}\dot{x^c}=0## covariantly constant... -

MHB How Do You Calculate the Length of the Curve from $x=\ln{4}$ to $x=\ln{5}$?
$\textsf{12 Find the length of the curve $y=\ln(e^x-1)-\ln( e^x+1 )$ from $x=\ln{4}$ to $x=\ln{5}$}$ ok I thot that curve lengths were done with parametric equations but didn't know how to convert this -
D
Finding the volume surrounded by a curve using polar coordinate
Homework Statement I tried to answer the following questions is about the curve surface z= f (x, y) = x^2 + y^2 in the xyz space. And the three questions related to each otherA.) Find the tangent plane equation at the point (a, b, a^2+ b^2) in curved surface z . The equation of the...- devinaxxx
- Thread
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-

Can a Body of Water's Temperature Rise Linearly with Constant Heating?
I'm trying to guess when my hot tub will be ready for use. If an ideal body of water is insulated and has a constant source of heating applied to it, can its temperature be expected to rise linearly? (No. Even as I write this I see it can't be true. As the water temp rises, it will approach...- DaveC426913
- Thread
- Replies: 19
- Forum: Thermodynamics
-
F
I Finding the Right Curve Fit: A Question About Curve Fitting
Hello everyone, A question about curve fitting. Hope you can share some helpful hints. Given some data we plot a graph y versus x. How do we approach the problem from a curve fitting standpoint? For example, using Excel, if the data "looks" linear from the graph, we choose a linear fit and...- fog37
- Thread
-
- Tags
- Curve Curve fitting Fit Fitting
- Replies: 16
- Forum: General Math
-
W
What is the equation of this stress-strain curve?
For this nonlinear hardening stress strain curve, how do you express strain in terms of stresses ?- wh88
- Thread
- Replies: 1
- Forum: Mechanical Engineering
-
H
How do you find a curve pipe bending moment and shear force?
1. Homework Statement I have problem solving the bending moment and shear force of a conduit with a curve end. The conduit is lifted in the mid-air with 2 slings and assume it is in equillibrum. I have attach a drawing for reference. Homework Equations What i know, there is a UDL somewhere...- HHJ
- Thread
- Replies: 9
- Forum: Engineering and Comp Sci Homework Help
-

I Stress Strain Curve: How Is It Derived & Tested?
hi, I am aware that stress strain curve involves some function which begins with linear part and continues with non linear part after a while. I consider that it is so complicated, but I really wonder how a stress strain curve is derived, what kind of tests are applied and how those tests are...- mertcan
- Thread
- Replies: 4
- Forum: Other Physics Topics
-
M
MHB How to Find the Curve σ from Intersection of Surfaces?
Hey! :o I want t calculate $\int_{\sigma}(ydx+zdy+xdz)$ when $\sigma$ is the curve that traces once the intersection of the surfaces with equations $x+y=2$ and $x^2+y^2+z^2=2(x+y)$ with positive direction while we look the traces from the point $(0,0,0)$. We have that... -

MHB 13.4.7 Find the curvature of the curve r(t).
$\textit{$13.4.7$ Find the curvature of the curve $r(t).$}$ \begin{align*}\displaystyle r(t)&=(5+9 \cos 8t) i - (4 + 9 \sin 8t)j + 6k\\ v&= -72\sin(8t)+72\cos(8t)\\ |v|&=\sqrt{(-72\sin(8t))^2 +(72\cos(8t))^2}\\ &=5184\\ \frac{v}{|v|}&=\frac{-72\sin(8t)+72\cos(8t)}{5184}\\... -

How can I determine the curve and tension in a hammock with damaged cords?
Homework Statement You want to rest on a hammock where the cords are damaged. a) If you don't want to the cords to break during your nap, do you have to place the hammock at the horizontal or, on the contrary, put the knot of the first rope higher than the other ? b) What is the curve made by...- ShaddollDa9u
- Thread
-
- Tags
- Curve
- Replies: 1
- Forum: Introductory Physics Homework Help
-
A
B What is the Net Force on a Banked Curve?
I understand why when deriving the formulas for cars on banked curves, the net force in the Y direction is zero. However, when I google how to derive them, people say that there is a net force greater than zero in the X direction. This is not what my professor says in his explanations however...- Abu
- Thread
- Replies: 3
- Forum: Classical Physics
-

Parametrize the Curve of Intersection
Hi everyone! I'm a student of electrical engineering. At my math class, we were given a problem to solve at home. Now, from what I've managed to gather, this is a trick question, but I would like to get someone else's opinion on the task. It's also worth mentioning that parametrization is a...- peroAlex
- Thread
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
B
Area under the curve of a mass time graph
Homework Statement Homework Equations Force * time = mass * change in velocity[/B]The Attempt at a Solution What I did was I converted the y-axis from kilograms to Newtons, since the "mass" reading is the force that the scale experiences. Then, the area under the curve will be the change... -

Car on Banked Curve: Centripetal Force?
Does a car on a banked curve have a component of gravity that accounts for the centripetal force ( along with the normal force)?- starstruck_
- Thread
-
- Tags
- Banked curve Car Curve
- Replies: 24
- Forum: Mechanics
-
T
Understanding the Concept of Double Mass Curve Analysis
Homework Statement In this first photo , we can see that the adjusted is found by extending the longer portion of straight line . The line is extended to the upper part of the graph.( We can see that there's a break in the line , the longer portion of the line is extended , and taken as...- tzx9633
- Thread
- Replies: 9
- Forum: Engineering and Comp Sci Homework Help
-
P
How do I calculate the output curve of a crank?
I am having a difficult time communicating about concepts without the math. And I have some very specific questions. So here we go with one of them. Regarding a crank mechanism, say with a throw of 10 centimeters, how can I calculate what percentage of a given constant force that is applied...- poe
- Thread
- Replies: 4
- Forum: Mechanical Engineering
-
S
Relationship Graph Between Frequency and Tension
Homework Statement After plotting a graph with frequency (f) of a wire on the y-axis and tension (C-Clamps) on the x-axis, a root curve was obtained. If the trend of the line is maintained, does it pass through the origin? Should it? Note: graph attached Homework Equations f is proportional...- Stormblessed
- Thread
- Replies: 10
- Forum: Introductory Physics Homework Help
-
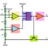
A particle travels along a plane curve (Polar coordinates)
Homework Statement 13.24 A particle travels along a plane curve. At a certain instant, the polar components of the velocity and acceleration are vR=90mm/s, vθ=60mm/s, aR=-50mm/s2, and aθ=20mm/s2. Determine the component of acceleration that is tangent to the path of the particle at this...- Alexanddros81
- Thread
- Replies: 6
- Forum: Introductory Physics Homework Help
-

Pen P of the flatbed plotter traces the curve - Path Coordinates
Homework Statement This is Pytels Dynamics 2nd edition problem 13.16 13.16. Pen P of the flatbed plotter traces the curve y=x3/80000, where x and y are measured in mm. When x=200mm, the speed of slider A is 60 mm/s. For this position, calculate (a) the speed of P; and (b) the normal component...- Alexanddros81
- Thread
-
- Tags
- Coordinates Curve Kinematics Path
- Replies: 3
- Forum: Introductory Physics Homework Help
-

MHB Particle Motion in a Vertical Plane: Trajectory Equation & Curve
A particle moves in a vertical plane from rest under the influence of gravity and a force perpendicular to and proportional to its velocity. Obtain the equation of the trajectory, and identify the curve.- lfdahl
- Thread
- Replies: 10
- Forum: General Math
-
S
Master Curve Sketching 1: Tips and Tricks for Perfect Graphs
1 The attempt at a solution: For part a) I got the following: I'm stuck on part b). I've tried to take the maclaurin series of coth x to see what the function does when T→0 and T→∞- subzero0137
- Thread
-
- Tags
- Curve
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
K
Line passing through a point and normal to a curve
Homework Statement What is the equation of a straight line passing through (1,2) and normal to ##~x^2=4y## Homework Equations Slopes of perpendicular lines: $$m_2=-\frac{1}{m_1}$$ The Attempt at a Solution $$x^2=4y~\rightarrow~m_1=y'=\frac{x}{2}$$ $$m_2=-\frac{2}{x}$$... -
S
MATLAB Weighting data points with fitted curve in Matlab
Hi all, I'm currently in the middle of performing an experiment for the final project of my MSc, and I have a question about how I should go about weighting the data when fitting a curve to it using the MATLAB fitting tool. Firstly, a bit of background about the problem. I am seeing how low...- Steven Thomas
- Thread
- Replies: 6
- Forum: MATLAB, Maple, Mathematica, LaTeX
-
A
Friction guiding a car around a curve
friction is causes the circular motion in the car around a curve, and if we draw free body diagram we will see the friction force must be opposite the car motion so the force of friction not toward to the center of the curve ,so the force of friction must be not the centripetal force ,mustn't it?- ahmed emad
- Thread
- Replies: 1
- Forum: Mechanics
-
A
Alternative approach -- Bicycle on a curve
Homework Statement A bicycle of mass m is traveling at constant speed v around a curve of radius r without slipping. You can take the acceleration due to gravity as g. Calculate the angle of tilt, θ, that will enable it to balance. Homework Equations R=mg Rsintheeta (Length)=Fcostheeta... -
J
I How to calculate the area under a curve
I was doing some integral exercises for getting area under the function. I was doing only more simple stuff, like functions that don't go over the same "x area" multiple times, like a quadratic function. My question is how to calculate area of a loop in an equation x^3+y^3-3axy=0 if let's say... -

What is the radius of the circular arc in a sine curve trajectory?
Homework Statement Homework EquationsThe Attempt at a Solution Every small part of the trajectory can be taken as a circular arc. Then, $$\frac { m v^2} R ≤ kmg $$ But how to find out R from the sine-curve?- Pushoam
- Thread
-
- Tags
- Curve Sine Trajectory
- Replies: 14
- Forum: Introductory Physics Homework Help
-
D
Specific heat in the curve of equilibrium
Homework Statement Consider a system formed by two phases of a substance that consists of a single class of molecules. Determine the specific heat ##c## of a vapor pressure and temperature ##p## ##T## on the curve of liquid-vapor equilibrium. Consider the steam as an ideal gas. Data: ##c_p##...- Dario SLC
- Thread
- Replies: 1
- Forum: Introductory Physics Homework Help
-
H
Branched-line pumping system curve help
Hi all, I am a student trying to figure out the system curve for a pipe line system. I know how to calculate friction loss for just one flow, but not for a system of branched flow! I read a short article online saying that for parallel pipes the friction head is the same for all branches, so...- help_pls
- Thread
- Replies: 1
- Forum: Mechanical Engineering
-
R
Potential energy vs position curve
Can a potential energy curve be vertical ?