Why Does the Order of Transformations Affect the Graph of a Function?

[modonnell121]

Okay so I've done very well in college so far, and I thought I was at least decent at math, but I just started this precalculus class and I'm having an issue.

I basically don't know, and can't get a straight answer about how to handle functions that have multiple transformations going on. This is not a homework question, but it is a perfect example of my issue, so I'm posting it.

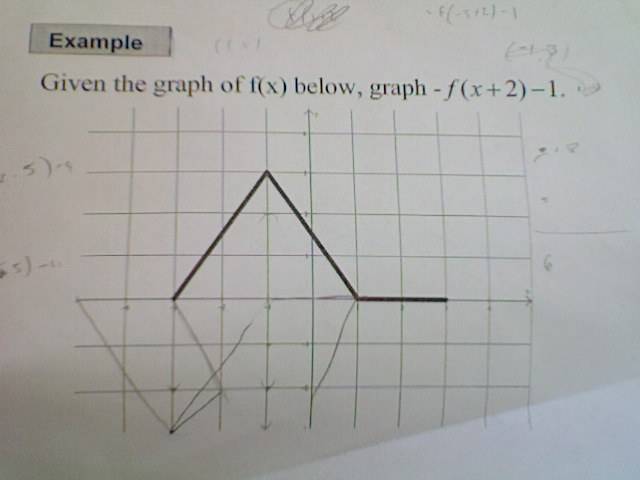
My answer is the function sketched below and to the left of the printed one, except I would have shifted it down one but there is no room on the graph, as you can see. I must be that far off, huh? The teacher's answer is like mine but shifted up one unit. This is apparently because he reflected it after shifting, while I reflected first. In his email explaining why he did this he told me "It's always best to do the reflecting last as it is the last thing that happended to the function in the transformation process." WHAT?

How do I know the order, what do I DO? Please someone help me.

 

[Matt Benesi]

I believe your teacher is wrong, and you are correct (unless I'm suffering from brain failure).

In the case of y= -f(x+2) -1 you must "reflect" f(x+2) before subtracting 1! This graph should be 1 below y= -f(x+2)!

If it was y= - [f(x+2) -1] you would "reflect" afterwords like your teacher did (ultimately shifting up 1, because y = - [f(x+2) -1] = -f(x+2) + 1).

 

[modonnell121]

Cool, I thought I was right. But can you explain how I determine the order to do the transformations in general?

 

[Matt Benesi]

Cool, I thought I was right. But can you explain how I determine the order to do the transformations in general?

Sorry, didn't see your reply until today. There is a specific order of operations, with a few different rules to get used to.

For functions (such as f(x) or g(x)), you apply the function to whatever is within the parenthesis in the function declaration.

f(x) you apply the function f to x

f(x+2) you apply the function f to x+2. in other words you replace the value for x with x+2

IF f(x) = 2x THEN f(x+2) = 2(x+2)

IF f(x) = 2x+1 THEN f(x+2) = 2(x+2) + 1 etc.

Then you follow the standard order of operations.

IF y=f(x) + 1 you calculate f(x) then add in 1 to calculate y.

IF y=-f(x) + 1 you calculate -f(x) then add in 1 to calculate y.

IF y=-[f(x) + 1] you calculate f(x), add in 1, and THEN flip the sign to determine your y value.

 

[CellCoree]

I understand that it can be frustrating when learning new concepts in math. However, it is important to remember that understanding the order of transformations in a function is crucial in accurately graphing it. The general rule is to perform the transformations in the following order: 1) horizontal shifts, 2) vertical shifts, 3) reflections, and 4) stretches or compressions.

In the example you provided, it seems that you correctly performed the reflection first and then the vertical shift. However, your teacher's approach of performing the vertical shift first and then the reflection is also correct. This is because the order in which transformations are performed does not affect the final result, as long as all the transformations are done correctly.

To determine the order of transformations, it is important to understand the effects of each transformation on the graph. For example, a horizontal shift will move the graph left or right, a vertical shift will move the graph up or down, a reflection will flip the graph across a line, and a stretch or compression will change the shape of the graph.

One strategy to help remember the order is to think about the order in which these transformations physically occur. For example, if you were to physically perform these transformations on a piece of paper, you would first move the paper left or right (horizontal shift), then move it up or down (vertical shift), then flip it over (reflection), and finally stretch or compress it (stretch or compression).

I recommend practicing with different functions and identifying the order of transformations to solidify your understanding. Additionally, do not hesitate to ask your teacher for clarification if you are still unsure. With practice and understanding of the order of transformations, I am confident you will improve in graphing functions with multiple transformations.