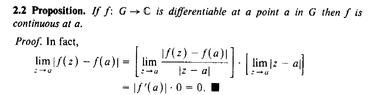Understanding Differentiability and Continuity in Complex Analysis

In summary, the two books discuss the proofs that for a function of a complex variable, differentiability implies continuity. While the proofs presented by John B. Conway and John H. Mathews and Russel W. Howell (M&H) are slightly different, they are both correct and equivalent. The main difference is that Conway uses modulus/norm signs in his proof, while M&H do not. Some may argue that Conway's inclusion of these signs is unnecessary, but it ultimately does not affect the validity of the proof.
  • #1
Math Amateur
Gold Member
MHB
3,998
48
I have been reading two books on complex analysis and my problem is that the two books give slightly different and possibly incompatible proofs that, for a function of a complex variable, differentiability implies continuity ...

The two books are as follows:

"Functions of a Complex Variable I" (Second Edition) ... by John B. Conway

"Complex Analysis for Mathematics and Engineering" by John H. Mathews and Russel W. Howell (M&H) [Fifth Edition] ... Conway's proof that for a function of a complex variable, differentiability implies continuity ... reads as follows:
View attachment 9258
Mathews and Howell's proof that for a function of a complex variable, differentiability implies continuity ... reads as follows:
View attachment 9259
Now, as can be seen in the above proofs, Conway uses modulus/norm signs around the expressions in the proof while Mathews and Howell do not ...Can someone explain the differences ... are both correct ... ?

Surely the Conway proof is more valid as the proof involves limits which involve ideas like "close to" which need modulus/norms ...Hope someone can clarify this issue ...

Peter
 

Attachments

  • Conway - Proposition 2.2 .png
    Conway - Proposition 2.2 .png
    5.1 KB · Views: 80
  • M&H - Theorem 3.1 ... .png
    M&H - Theorem 3.1 ... .png
    13.7 KB · Views: 104
Physics news on Phys.org
  • #2
They are equivalent. If [tex]\lim_{x\to a} f(x)= b[/tex] then [tex]\lim_{x\to a} |f(x)|= |b|[/tex] and if b= 0 the converse is also true.
 
  • #3
HallsofIvy said:
They are equivalent. If [tex]\lim_{x\to a} f(x)= b[/tex] then [tex]\lim_{x\to a} |f(x)|= |b|[/tex] and if b= 0 the converse is also true.

Thanks for the help HallsofIvy ...

But ... it leaves me thinking that Conway made a pointless elaboration of his proof as modulus/norm signs were unnecessary ... indeed, I have no idea why he included them ...

Peter
 

Related to Understanding Differentiability and Continuity in Complex Analysis

What is the definition of differentiability in complex analysis?

In complex analysis, differentiability refers to the property of a complex-valued function of having a derivative at a point. This means that the function is smooth and has a well-defined slope at that point.

How is differentiability related to continuity in complex analysis?

Differentiability and continuity are closely related in complex analysis. A function is differentiable at a point if and only if it is continuous at that point. This means that if a function is not continuous at a point, it cannot be differentiable at that point.

What is the Cauchy-Riemann equations and how do they relate to differentiability?

The Cauchy-Riemann equations are a set of necessary and sufficient conditions for a complex-valued function to be differentiable at a point. These equations relate the partial derivatives of the real and imaginary parts of a function, and if they are satisfied, the function is differentiable at that point.

Can a function be differentiable but not analytic?

Yes, a function can be differentiable at a point but not analytic in a neighborhood of that point. This means that the function does not have a power series expansion around that point, and therefore cannot be represented as a complex polynomial.

What are the implications of a function being analytic in a region?

If a function is analytic in a region, it means that it is differentiable at every point in that region, and can be represented as a complex polynomial. This has important implications in complex analysis, as it allows for the use of powerful tools such as Cauchy's integral theorem and Cauchy's integral formula.

Similar threads

MHB Understanding Theorem 3.4: Mean Value Theorem & Cauchy Riemann Equations
    • Topology and Analysis
Replies
2
Views
930
MHB Parametrization Of Complex Curves .... Mathews And Howell, Example 1.22 .... ....
    • Topology and Analysis
Replies
2
Views
1K
MHB Continuity of a Function .... Conway, Definition 1.7.1 .... ....
    • Topology and Analysis
Replies
3
Views
1K
I Limits of Functions ....Conway, Proposition 2.1.2 .... ....
    • Topology and Analysis
Replies
7
Views
2K
MHB Limits of Functions ....Conway, Proposition 2.1.2 .... ....
    • Topology and Analysis
Replies
1
Views
981
MHB Complex Valued Functions BV: John B. Conway Prop 1.3 Explained
    • Topology and Analysis
Replies
3
Views
1K
I On differentiability and Fourier coefficients (Vretblad's text)
    • Topology and Analysis
Replies
4
Views
398
MHB The Riemann Integral .... Conway, Proposition 3.1.4 ....
    • Topology and Analysis
Replies
2
Views
1K
I Complex & Real Differentiability ... Remmert, Section 2, Ch 1
    • Topology and Analysis
Replies
4
Views
2K
MHB Complex and Real Differentiability .... Remmert, Section 2, Ch. 1 .... ....
    • Topology and Analysis
Replies
1
Views
1K

Hot Threads

Recent Insights

Back
Top