Limits of Functions ....Conway, Proposition 2.1.2 .... ....

[Math Amateur]

TL;DR Summary

I need help with the logic of the proof of John Conway's proof of a Proposition concerning the limit of a function ...

I am reading John B. Conway's book: A First Course in Analysis and am focused on Chapter 2: Differentiation ... and in particular I am focused on Section 2.1: Limits ...

I need help with an aspect of the proof of Proposition 2.1.2 ...Proposition 2.1.2 and its proof read as follows:

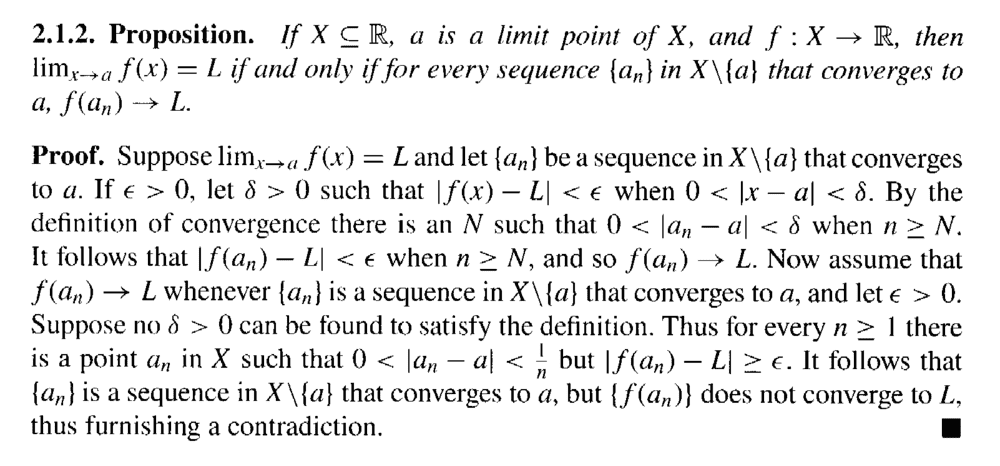
In the above proof by Conway we read the following:

" ... ... Now assume that ##f(a_n) \to L## whenever ##\{ a_n \}## is a sequence in ##X##\##\{a\}## that converges to ##a##, and let ##\epsilon \gt 0##. Suppose no ##\delta \gt 0## can be found can be found to satisfy the definition. ... ... "
Above Conway seems to me that he is assuming that ##f(a_n) \to L## and then assuming that the definition of ##f(a_n) \to L## doesn't hold true ... which seems invalid ...

Can someone explain Conway's logic ... can someone please explain what is actually being done in this part of the proof ...

Peter

 

[Mark44]

This is an "if and only if" proof. To prove P iff Q, you need to do two proofs. First, assume that P is true, and show that Q must also be true. Second, assume that Q is true, and then show that P is also true.

 

[member 587159]

This implication of the proof is written down very badly imo.

The author proves an implication using contraposition/contradiction.

We prove ##\lim_{x\to a} f(x)\neq L## implies that there is a sequence ##(a_n)_n## in ##X\setminus \{a\}## with ##a_n\to a## but with ##f(a_n)\not\to L##. Using contraposition on this statement, one of the implications follows.

So let's begin. Our assumption that the limit does not exist means:

##\exists \epsilon >0: \forall \delta >0: \exists x\in X\setminus \{a\}: |x-a|<\delta \land |f(x)-L|\geq \epsilon##

(This is just the negation of the definition of limit).

Fix an ##\epsilon## as above (this Conway's first unclarity: we can't take an arbitrary ##\epsilon##).

Put ##\delta_n:= 1/n## for ##n\geq 1## and choose an associated sequence ##(x_n)_n## in ##X## with ##0<|x_n-a|<\delta_n## and ##|f(x_n)-L|\geq \epsilon##. Letting ##n\to \infty##, we see that ##x_n\to a## but ##f(x_n)\not\to L##, as desired.

 

[member 587159]

This is an "if and only if" proof. To prove P iff Q, you need to do two proofs. First, assume that P is true, and show that Q must also be true. Second, assume that Q is true, and then show that P is also true.

Yes but this is not the structure of the author's proof. Rather the author proves P is not true implies Q is not true (contraposition) which is of course equivalent with Q is true implies P is true.

 

[PeroK]

Above Conway seems to me that he is assuming that ##f(a_n) \to L## and then assuming that the definition of ##f(a_n) \to L## doesn't hold true ... which seems invalid ...

Can someone explain Conway's logic ... can someone please explain what is actually being done in this part of the proof ...

He is assuming that for every sequence ##f(a_n) \to L##, but yet ##\lim_{x \rightarrow a} f(x) = L## is not true.

Note that the proposition says that these two things are equivalent. Their definitions are quite similar and to accept one and deny the other leads quickly to a contradiction.

 

[Mark44]

Yes but this is not the structure of the author's proof. Rather the author proves P is not true implies Q is not true (contraposition) which is of course equivalent with Q is true implies P is true.

I understand this. My point was that for an iff proof, you have to prove both statements by some means. I didn't include all of the possibilities; i.e., direct proof, contrapositive proof, proof by contradiction.

 

[Math Amateur]

This implication of the proof is written down very badly imo.

The author proves an implication using contraposition/contradiction.

We prove ##\lim_{x\to a} f(x)\neq L## implies that there is a sequence ##(a_n)_n## in ##X\setminus \{a\}## with ##a_n\to a## but with ##f(a_n)\not\to L##. Using contraposition on this statement, one of the implications follows.

So let's begin. Our assumption that the limit does not exist means:

##\exists \epsilon >0: \forall \delta >0: \exists x\in X\setminus \{a\}: |x-a|<\delta \land |f(x)-L|\geq \epsilon##

(This is just the negation of the definition of limit).

Fix an ##\epsilon## as above (this Conway's first unclarity: we can't take an arbitrary ##\epsilon##).

Put ##\delta_n:= 1/n## for ##n\geq 1## and choose an associated sequence ##(x_n)_n## in ##X## with ##0<|x_n-a|<\delta_n## and ##|f(x_n)-L|\geq \epsilon##. Letting ##n\to \infty##, we see that ##x_n\to a## but ##f(x_n)\not\to L##, as desired.

Thanks for a very helpful and clear explanation ...

I must say that Conway did not explain things very well ...

I think I'll switch to another text ...

Peter

 

[Math Amateur]

Thanks to Math_QED, Mark44 and PeroK for your help ...

Peter