Supremum Property, Archimedean Property, Nested Intervals

[Math Amateur]

I am reading Houshang H. Sohrab's book: "Basic Real Analysis" (Second Edition).

I am focused on Chapter 2: Sequences and Series of Real Numbers ... ...

I need help with Theorem 2.1.45 concerning the Supremum Property (AoC), the Archimedean Property, and the Nested Intervals Theorem ... ...

Theorem 2.1.45 reads as follows:

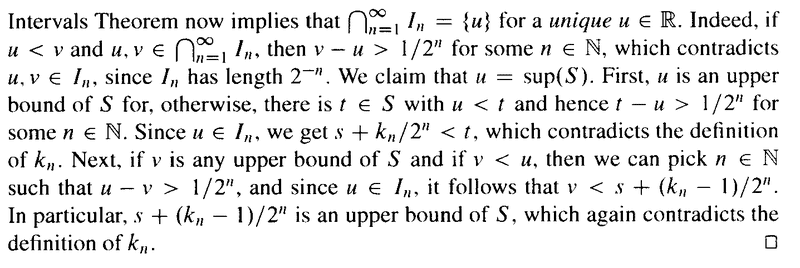My questions regarding the above text from Sohrab are as follows:Question 1

In the above text we read the following:

" ... ... ##s + \frac{m}{ 2^n}## is an upper bound of ##S##, for some ##m \in \mathbb{N}##. Let ##k_n## be the smallest such ##m## ... ... "Can we argue, based on the above text, that ##s + \frac{m}{ 2^n} = \text{Sup}(S)## ... ... ?
Question 2

In the above text we read the following:

" ... ... We then have ##I_n \cap S \ne \emptyset##. (Why?) ... ... "Is ## I_n \cap S \ne \emptyset## because elements such as ##s + \frac{ k_n - x }{ 2^n} , \ 0 \lt x \lt 1## belong to ##I_n \cap S## ... for example, the element ##s + \frac{ k_n - 0.5 }{ 2^n} \in I_n \cap S##?

Is that correct ... if not, then why exactly is ##I_n \cap S \ne \emptyset##?Hope someone can help ...

Peter==============================================================================

The above theorem concerns the Supremum Property, the Archimedean Property and the Nested Intervals Theorem ... so to give readers the context and notation regarding the above post I am posting the basic information on these properties/theorems ...

 

[andrewkirk]

Question 1

In the above text we read the following:

" ... ... ##s + \frac{m}{ 2^n}## is an upper bound of ##S##, for some ##m \in \mathbb{N}##. Let ##k_n## be the smallest such ##m## ... ... "Can we argue, based on the above text, that ##s + \frac{m}{ 2^n} = \text{Sup}(S)## ... ... ?

No. Consider ##S=\{x\in\mathbb R\ :\ x<\sqrt 2\}## and ##s=1##. The supremum of this ##S## is ##\sqrt 2##, which is irrational, while ##s+m/2^n## is rational for any ##m,n\in\mathbb N##.

The idea is that the two endpoints of the interval ##I_n## will straddle the supremum of ##S##.

Question 2

In the above text we read the following:

" ... ... We then have ##I_n \cap S \ne \emptyset##. (Why?) ... ... "Is ## I_n \cap S \ne \emptyset## because elements such as ##s + \frac{ k_n - x }{ 2^n} , \ 0 \lt x \lt 1## belong to ##I_n \cap S## ... for example, the element ##s + \frac{ k_n - 0.5 }{ 2^n} \in I_n \cap S##?

Is that correct ... if not, then why exactly is ##I_n \cap S \ne \emptyset##?

Because, if the set were empty, then ##s+(k_n-1)/2^n##, the lower bound of ##I_n##, would be an upper bound for ##S##, which would contradict the assumption that ##k_n## is the smallest natural number ##m## such that ##s+m/2^n## is an upper bound for ##S##.

 

[Math Amateur]

No. Consider ##S=\{x\in\mathbb R\ :\ x<\sqrt 2\}## and ##s=1##. The supremum of this ##S## is ##\sqrt 2##, which is irrational, while ##s+m/2^n## is rational for any ##m,n\in\mathbb N##.

The idea is that the two endpoints of the interval ##I_n## will straddle the supremum of ##S##.Because, if the set were empty, then ##s+(k_n-1)/2^n##, the lower bound of ##I_n##, would be an upper bound for ##S##, which would contradict the assumption that ##k_n## is the smallest natural number ##m## such that ##s+m/2^n## is an upper bound for ##S##.

Hi Andrew,

Thanks for the help ... but ...

... I understand your first statement ... but then you write:

" ... ... The idea is that the two endpoints of the interval ##I_n## will straddle the supremum of ##S##."

Surely the supremum will be at or beyond the right endpoint ... and not straddle the left and right endpoints ...

Can you clarify further ...

Peter

 

[andrewkirk]

The right endpoint is ##Hi=s+k_n/2^n##, which is an upper bound for ##S##, and the left endpoint is ##Lo=s+(k_n-1)/2^n##, which is not.

If ##u## is the supremum of ##S## then ##u\leq Hi## since a supremum (least upper bound) cannot be greater than any other UB.
Since ##Lo## is not a UB of ##S## while ##u## is, we must have ##Lo<u##.
Hence ##Lo<u\leq Hi##, whence ##u\in (Lo,Hi]\subset [Lo,Hi]=I_n##.

 

[Math Amateur]

Thanks Andrew ... that clarifies the issue ...

Peter