Laplace Transfrom to Solve ODE Help

[mmmboh]

Hi, so we just started learning about Laplace transforms yesterday, and I have a problem which I am not sure what to do:

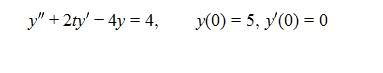
My question is about the second term, if it was a constant coefficient I could do this fine, but none of the 2 examples we did in class for solving ODEs with Laplace transforms involved non-constant coefficients...so I'm not sure how to deal with that term, I tried something with integration by parts, but that didn't work..and I don't suppose I can just pretend t is constant and bring it outside the Laplacian.

Can someone tell me how I am suppose to deal with the 2ty' term please?

Thanks!

 

[Jerbearrrrrr]

You should have a list of transforms (assuming you don't want to derive the transform from scratch, which...isn't hard, but it's integration by parts which is eww).

Do you know the transform of y' in terms of the transform of y?
Do you know the transform of tf in terms of the transform of f?

[edit] Sorry, I only skimmed your post. Bad me. Integration by parts should work! Be careful though. Minus signs and stuff arghh.

 

[mmmboh]

Yes I know the transform of y' in terms of the transform of y, but I don't know the transform of tf in terms of the transforms of f, we didn't get to that...that would help. I'm not sure I did the integration by parts right, I'll try again.

 

[mmmboh]

Ok well I have derived that L(ty)=t*L(y)-integral(L(y))...but I'm not sure that helps.

Would the integral of L(y)dt just be t*L(y)? since L(y) is not a function of t?

 

[vela]

Ok well I have derived that L(ty)=t*L(y)-integral(L(y))...but I'm not sure that helps.

Would the integral of L(y)dt just be t*L(y)? since L(y) is not a function of t?

Hmm, that looks backward.

[tex]L[ty] = \int_0^\infty ty e^{-st}dt = \int_0^\infty \left(-\frac{\partial}{\partial s}\right)ye^{-st}dt = -\frac{\partial}{\partial s} \int_0^\infty ye^{-st}dt[/tex]