Can I Use Logarithms to Solve Exponential Equations?

[Kevin Licer]

So, recently I have been learning about logarithms and how to solve exponential equations with the help of logarithms, but I am curious if I can take the log of both sides of an equation like this in order to solve it?

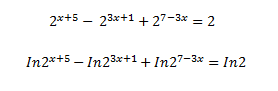
If not, then could someone explain why? Thanks.

 

[Orodruin]

You cannot, the logarithm of a sum is not equal to the sum of the logarithms of the individual terms.

 

[Kevin Licer]

So, taking the log of both sides of this equation would be more like this?

And would it be useful in this case?

 

[Orodruin]

Yes.

 

[Mentallic]

So, taking the log of both sides of this equation would be more like this?
View attachment 89007And would it be useful in this case?

Yes, that would be the correct way to take the log of both sides, but since you can't do anything with that log on the left because of all the summed terms in its argument, you similarly are stuck at solving this problem. It's a very difficult one to solve that's outside of the scope of what you're doing. You can get lucky and find an easy interger solution though (although this isn't the only solution and you won't be finding the others).

 

[Mark44]

So, taking the log of both sides of this equation would be more like this?
View attachment 89007And would it be useful in this case?

Yes.

Orodruin's answer is a response to the first question, I'm pretty sure. As for the second question, would it be useful?
No, for the reason already given, that the log of a sum can't be simplified further.

 

[Kevin Licer]

Yes, I see now, I thought I could solve the equation by taking the log of both sides, but seeing as that is a mistake I'll try and work it out another way. Thanks!

 

[Curious3141]

The most common way of solving a problem like this in an elementary fashion is to try to get it into the form of a polynomial equation that can be easily solved. Of course, the question has to be set specifically so that it's "easy" to solve that way, and in this case, it is.

You need to be familiar with the rules of exponentiation. These are what you need: ##a^{b+c} = a^b \cdot a^c## and ##a^{bc} = (a^b)^c##

Using those rules, you can convert your equation into a sextic (power-6) equation in terms of a new variable ##y##, where ##y = 2^x##. This equation (thankfully) has at least one nice integer solution, which you can quickly find by trial and error (aided by the Rational Root Theorem, http://www.purplemath.com/modules/rtnlroot.htm).

At this point you need to find the full solution set, or at least show there are no other real, positive solutions (since an exponential is strictly positive). You can do this by either polynomial long division or the much simpler synthetic division (http://www.purplemath.com/modules/synthdiv.htm) by the linear factor you uncovered in the last step to get a quintic (power-5) polynomial. It's "tough" to solve or even sketch this curve, but fortunately, there is a little trick called the Decartes' Rule of Signs (http://www.purplemath.com/modules/drofsign.htm) that allows you to very quickly conclude that the quintic has no positive real roots. Hence the single value for ##y## you've already found is the only one that is valid.

Finally, you find ##x## by solving ##2^x = y## for ##x##, which I assume you know to do. In the general case you can do so by taking logs of both sides, but here all that's required is simple inspection (this should give you a big hint about how "nice" the solution is).

(Edited for more details, since I was rushing to work in the morning and was unable to complete the post).