What is Distribution: Definition and 1000 Discussions

The Cauchy distribution, named after Augustin Cauchy, is a continuous probability distribution. It is also known, especially among physicists, as the Lorentz distribution (after Hendrik Lorentz), Cauchy–Lorentz distribution, Lorentz(ian) function, or Breit–Wigner distribution. The Cauchy distribution



f
(
x
;

x

0


,
γ
)


{\displaystyle f(x;x_{0},\gamma )}
is the distribution of the x-intercept of a ray issuing from



(

x

0


,
γ
)


{\displaystyle (x_{0},\gamma )}
with a uniformly distributed angle. It is also the distribution of the ratio of two independent normally distributed random variables with mean zero.
The Cauchy distribution is often used in statistics as the canonical example of a "pathological" distribution since both its expected value and its variance are undefined (but see § Explanation of undefined moments below). The Cauchy distribution does not have finite moments of order greater than or equal to one; only fractional absolute moments exist. The Cauchy distribution has no moment generating function.
In mathematics, it is closely related to the Poisson kernel, which is the fundamental solution for the Laplace equation in the upper half-plane.
It is one of the few distributions that is stable and has a probability density function that can be expressed analytically, the others being the normal distribution and the Lévy distribution.

View More On Wikipedia.org
Recent contents Top users
  1. M

    I Linear regression and probability distribution

    I have some data that I want to do simple linear regression on. However I don't have a lot of datapoints, and would like to know the uncertainty in the parameters. I.e. the slope and the intercept of the linear regression model. I know it should be possible to get a prob. distribution of the...
  2. J

    A High-energy tail of H electron momentum distribution? 1/p^6?

    Kind of the basic question of atomic physics is momentum distribution of single electron of ground state hydrogen atom - especially the power in its high-energy tail (HTMD: high-tail momentum distribution), which should have strong impact especially on various scattering experiments. Fock's 1935...
  3. O

    Exponential Distribution, Mean, and Lamda confusion

    Homework Statement Accidents at a busy intersection follow a Poisson distribution with three accidents expected in a week. What is the probability that at least 10 days pass between accidents? Homework Equations F(X) = 1- e-λx μ = 1/λ The Attempt at a Solution Let x = amount of time between...
  4. D

    MCNP5 error: Source distribution in 2 volumetric cells (help please)

    Hello, can you help me? In my model, I have to simulate source distribution in two volumetric cells (30 and 31). For example, with a photon source of 356 keV, I have to simulate the distribution according 0.2 (20% in source 30: thyroid without nodule) and 0.8 (80% in source 31: nodule). I use...
  5. C

    Question about uniform charge distribution

    1. The problem statement, all variables, and given/known data Suppose you have a wire of length l and a uniform line charge density λ. Find the electric field at the midpoint that is height r above the x-axis Homework Equations (see attached) The Attempt at a Solution To solve, I used the...
  6. O

    Why isn't this a binomial distribution?

    Homework Statement An ordinary die is painted red on two sides, white on two sides and blue on two sides. Find the probability we get no reds in 12 rolls of the die. Homework EquationsThe Attempt at a Solution GENERAL QUESTION:[/B] I thought this would be a binomial distribution, but the book...
  7. Toby_phys

    Boltzmann vs Maxwell distribution?

    So I worked through the Boltzmann distribution and got: $$ P\propto e^{\frac{-E}{k_BT}} $$ Where $E$ is the energy. So surely this means the kinetic energy (and therefore speed) of particles is distributed over a Boltzmann distribution. Or in equation: $$ P\propto e^{\frac{-mv^2}{2k_BT}} $$...
  8. B

    "The distribution of heights is not Gaussian"

    I was browsing old threads at Physics Forums, and I came across some information in this thread from 2008 that got my interest. The thread is titled "Child molester avoids prison because he is short." PF member stickythighs wrote the following: "Since the average American man is 5'10", there...
  9. jdawg

    Statistics: Standard Deviation for a Normal Distribution

    Homework Statement A company allows a maximum failure rate of 1 out of 250,000 parts. To insure this quality goal, failed parts must be how many standard deviations from the mean? Use Excel to solve. Homework Equations z= (X-μ)/σ The Attempt at a Solution Hi! So I'm assuming that this is a...
  10. C

    Weight distribution on several floor anchors

    Hi all, I am not sure this is the right forum, but I guess my question fits better here than in classical physics. I am building a lightweight flooring in my utility room to store some "not very heavy" items. Two years back when my house was being finished, I installed two wooden wall plates...
  11. D

    Could a distribution of magnetic Dipoles create an Energy minimum

    The think is that I would like to create a magnetic trap "minimum of magnetic potential energy in all 3 directions of space" using a distribution of magnetic dipoles as a field generator. In other words, I would like to know if setting in some way some magnetic dipoles is possible to create a...
  12. Z

    75th percentile of the normal distribution

    Homework Statement The random variable X is normally distributed. The values 650 and 850 are at the 60th and 90th percentile of the distribution of X respectively. Find the value of the 75th percentile of the distribution of X. Homework Equations I found the above formula from internet. where...
  13. L

    I Is this a Poisson distribution problem?

    Hello, I have been thinking about this problem for a while, but I can't decide how it should be tackled statistically. I wonder if you can help, please. Suppose that prostheses for hip replacement are sold mainly by 2 manufacturers, A and B. Since they started being sold 20 years ago, 100 000...
  14. PePaPu

    Thermodynamic assembly - Statistical Thermodynamics

    Homework Statement Consider a model thermodynamic assembly in which the allowed (nondegenerate) states have energies 0, ε, 2ε, 3ε.The assembly has four distinguishable (localized) particles and a total energy U = 6ε. Tabulate the nine possible distributions of the four particles among the...
  15. J

    Average of cos(x)^2 in spherical distribution

    << Mentor Note -- Thread moved from the technical forums so no Homework Help Template is shown >> I'm particle physics at the moment and I don't get why the average value of cosˆ2 is 1/3. The section : My solution is : < cos^{2}(\alpha)> = \frac{1}{\pi - 0} \int_{0}^{\pi }...
  16. H

    Gauss's Law to find E with non-uniform charge distribution

    Homework Statement Hello, this is more of a conceptual question than a concrete homework assignment question. I'm learning about Gauss's law and the Prof did an exercise on a sphere with uniform charge distribution, where he found E(r). The trick was, that E(r) was constant over the Gaussian...
  17. Jamison Lahman

    What is the Intel Distribution for Python and how can it improve data analysis?

    Hello, I am relatively new to Python. I would really like to use Python for numerical and data analysis. I recently stumbled upon something called Intel Distribution from this article: http://www.infoworld.com/article/3117239/data-science/intels-python-distribution-turbocharges-data-science.html...
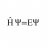
  18. H Psi equal E Psi

    Ideal gas pressure from Maxwell-Boltzmann distribution

    Hi everyone I'm having trouble with solving an exercise in statistical physics. I need to argue why the average number of particles with a velocity between ##v## and ##v+dv## that hit a surface area ##A## on the container wall in a time interval ##\Delta t## is $$N_{collision}=v_{x}A\Delta t...
  19. A

    I Density, distribution and derivative relationship (stats)

    I am currently enrolled in a statistics course, and the following is stated in my course book with no attempt at an explanation: Suppose that f is the probability density function for the random variable (X,Y), and that F is the distribution function. Then, f_{X,Y}(x,y)=\frac{\partial^{2}...
  20. David23454

    Find electric potential due to charge distribution

    Homework Statement In a certain region, the electric potential due to a charge distribution is given by the equation V (x, y, z) = (3x2y2+yz3-2z3x)V0/a4 where a, x, y, and z are measured in meters and V and V0 are in volts. What is the magnitude of the electric field at the position (x, y, z)...
  21. M

    "Immortal" jellyfish habitat range, Turritopsis dohrnii?

    What is the current habitat range of Turritopsis dohrnii or the "immortal" jellyfish? I know that there are multiple species of the Turritopsis genus and that the species dohrnii have recently increased its range by ballast water spread. What is the current range of the exact species dohrnii?
  22. mertcan

    I Weibull distribution derivation

    hi, I am looking for a proof of weibull distribution, I have searched a lot but nothing is reasonable for the proof, so ıs there derivation of this distribution ? What is the origin of this distribution ?
  23. C

    I Exponential Distribution Question

    Hi all, Can anyone teach me this problem ? Thanks The life of a tiger is exponentially distributed with a mean of 15 years.If a tiger is 10 years old, what is the expected remaining life of the tiger? A 5 years B 10 years C 15 years D Longer than 15 years
  24. rcgldr

    Pressure distribution for a ducted propeller

    Rather than going off topic in a thread about inviscid fluid in a pipe, I decided to start a new thread. For this thread, I'm wondering about the effect of a ducted propeller operating in the air. Using this NASA article as a guide: https://www.grc.nasa.gov/WWW/K-12/airplane/propanl.html The...
  25. J

    MHB Probability Distribution Problem

    Suppose that cars pass a certain intersection at a rate of 30 miles per hour. What is the probability that during a three-minute interval, no cars will pass the intersection? I am really just wondering which distribution to use. I thought is should be Poisson because it is asking for events...
  26. K

    What is the best way to determine the distributed load for a cargo shelf?

    Hello forum, I'm hoping i can get some help figuring something out. I'm working on a project which requires a 4 wheel trolley frame to be designed to transport cargo. The basic dimensions of the trolley I've already determined based on the required need and ergonomic guidelines etc. Now i need...
  27. A

    Convergence in distribution example

    Homework Statement Homework Equations [/B] Definition: A sequence X_1,X_2,\dots of real-valued random variables is said to converge in distribution to a random variable X if \lim_{n\rightarrow \infty}F_{n}(x)=F(x) for all x\in\mathbb{R} at which F is continuous. Here F_n, F are the...
  28. B

    MHB Normal Distribution: Percentiles

    The number of chocolate chips in a bag of chocolate chip cookies is approximately normally distributed with a mean of 1263 chips and a standard deviation of 117chips. ​(a) Determine the 26th percentile for the number of chocolate chips in a bag. ​(b) Determine the number of chocolate chips in...
  29. V

    Calculate vmax and voltage from X-ray distribution function

    Homework Statement The X-ray intensity distribution function for an X-ray lamp is given on the figure. What is the maximum velocity of the electrons? What is the potential difference under which the lamp is operating? Figure: http://imgur.com/01kCBc8 Homework Equations Kmax = 0.5m(vmax)^2...
  30. I

    B "Strength" of the mean of the distribution curve

    My understanding of the distribution curves is very basic but I do have a couple of somewhat generic questions. I looked up a number of definitions but have had a hard time finding these specific answers: - Is there an agreed on minimum number of samples that one needs to take to deem a result...
  31. davidge

    B "Distribution" of a particle in different situations

    I was thinking about the "distribution" of a particle in space in different situations. An electron bound in a atom have a wave function that is broad. What about the broadness of the wave function of conduction electrons in a wire? Or doesn't it even make sense to quantum-mechanicaly speak of...
  32. Euler2718

    I Hypergeometric Distribution Calculation in Libreoffice

    Given this libreoffice command: HYPGEOM.DIST(X; NSample; Successes; NPopulation; Cumulative) >X is the number of results achieved in the random sample. >NSample is the size of the random sample. >Successes is the number of possible results in the total population. >NPopulation is the size...
  33. R

    Electron distribution using tight binding band structure?

    Hi everyone, I am just wondering how to calculate electron distribution using tight binding band structure for a system like graphene or any other solid. So the goal is to get |\psi(r)|^2 which \psi is the band state and it is the linear combination of Bloch sum...
  34. F

    Understanding Carry-Over Factor in Beam Analysis

    Homework Statement I don't understand why for the first case , the 0.4 and 0.6 is used ? for the second question , we can see that in the first case , the moment from BC is carried over to CB ( highlighted part - line 4 ) ... Why for the second case , the moment from BC (6325.8) isn't carried...
  35. G

    Three-phase electric power: Household distribution

    Hi. How is three-phase electric power distributed in a household with mainly single-phase power plugs? Do they just connect a phase at random to every plug? As far as I understood, it's best if all three phases deliver the same current, since then neutral cancels. Do electricians take into...
  36. A

    A How to calculate RDF (Radial Distribution Function)

    Dear friends How can i calculate RDF(radial distribution function)? Thanks
  37. D

    Stat mech: Fermi-Dirac distribution

    Homework Statement Show that the FD distribution can be viewed as giving the probability that a given state ( of the prescribed energy) is occupied. Homework EquationsThe Attempt at a Solution Solution to this problem: I understand the solution,but I took a different approach...
  38. D

    A quick question about the Fermi-Dirac distribution

    Homework Statement An electron has two spin states and a set of energy levels E1,E2,... By the Fermi-dirac distrbution,the mean number of electrons in energy level Ek is https://en.wikipedia.org/wiki/Fermi–Dirac_statistics#Distribution_of_particles_over_energy Does it mean that,for an electron...
  39. D

    MHB Is the sampling distribution for skewness and kurtosis normal?

    The Central Limit Theorem specifically calls out a sample mean to be following normal distribution (for n>=30 ), But I am referring to certain text, and it is calculating z values for sample skewness and sample kurtosis assuming that these follow Normal distribution. Is it correct? In short...
  40. Charlie313

    Does a probability distribution correctly describe entropy?

    The colloquial statistical mechanics explanation of entropy as if it is caused by probability is dissatisfying to me, in part because it allows highly organized (i.e. with a real potential for work) arrangements to appear as 'random fluctuations', though with very low probability. But as far as...
  41. R

    Marginal Probability Distribution

    Homework Statement Two components of a laptop computer have the following joint probability density function for their useful lifetimes X and Y (in years): f(xy)=xe^(−x(1+y)) 0 <= x <= y 0 otherwise Find the marginal probability density function of X, fX(x). Enter a formula below. Use * for...
  42. Arman777

    Gauss' Law: Charge distribution on concentric spherical surfaces

    Homework Statement A metallic sphere of radius a is placed concentrically with a metallic spherical shell with inner radius b and outer radius c. The sphere has a total charge of 2Q and the shell has a total charge of 3Q. (a) What is the charge distribution? Specifically, what is...
  43. S

    A Using Fastjet in Pythia to plot distribution of particles

    I am using fastjet in pythia8.I am studying jet formation in pp collisions.I need to plot distribution of transverse momentum of fastest particle in fastest jet formed in 1000 events simulated.But i don't know how to access particle properties after jet formation.Like if I want to know the...
  44. CricK0es

    Derivative of Planck's spectral distribution

    Homework Statement From differentiating Planck's distribution and setting it equal to 0 I've reached the equation below. But now I'm asked to estimate the solution for a/λ. It's suggested that we try to do it graphically/trial and error as it's tricky to do analytically. I'm wondering how I...
  45. BrainMan

    Continuous Distribution of Charges Problem

    Homework Statement Charge Q is uniformly distributed along a thin, flexible rod of length L. The rod is then bent into the semicircle shown in the figure (Figure 1) . Find an expression for the electric field E⃗ at the center of the semicircle. Hint: A small piece of arc length Δs spans a...
  46. wolram

    B The distribution of normal matter precisely determines gravity

    I am unable to find a paper on this only the abstract, but it seems to be saying that there is no Dark Matter? The tightness of this relation is difficult to understand in terms of dark matter as it's currently understood, the researchers said. It also challenges the current understanding of...
  47. Cocoleia

    Electric field & energy in a spherical distribution of charge

    Homework Statement Homework Equations Gauss The Attempt at a Solution I am really confused with question a, I have an idea of how to answer b and c once I obtain an answer for part a... My best guess would be to use Gauss, but I am not sure. Would the field inside be 0? What will the bounds...
  48. Jamison Lahman

    Animal Intelligence Distribution

    My end goal is to extrapolate observed intelligences in the animal kingdom to determine whether or not it is statistically likely that a simulation argument is probable (though this could easily be used for the Fermi Paradox as well). Defining terms: "intelligence." Obviously all animals would...
  49. C

    Advice for 2x4 weight distribution....

    I have a 2x4 on it's edge that spans 10 feet in my ceiling. I want to hang a swing that can hold 250 pounds near the center of this span. What would I need to do in this situation in order to get minimal or no deflection?
  50. S

    I What is the significance of calculating the average value of cos?

    In kinetic theory, the number of molecules hitting a unit area of a surface per unit time with speeds between v and v + dv and angles between \theta and \theta + d \theta is found to be a function of sin(theta) and cos(theta). There will often be a practice problem asking to show that the...
Back
Top