- #1
DaveC426913
Gold Member
- 22,531
- 6,194
- TL;DR Summary
- How to apply rel. vel. addition in various geometrical scenarios
I keep getting into these discussions and finding out they are not as simple as I thought. Or at least, my math is rusty.
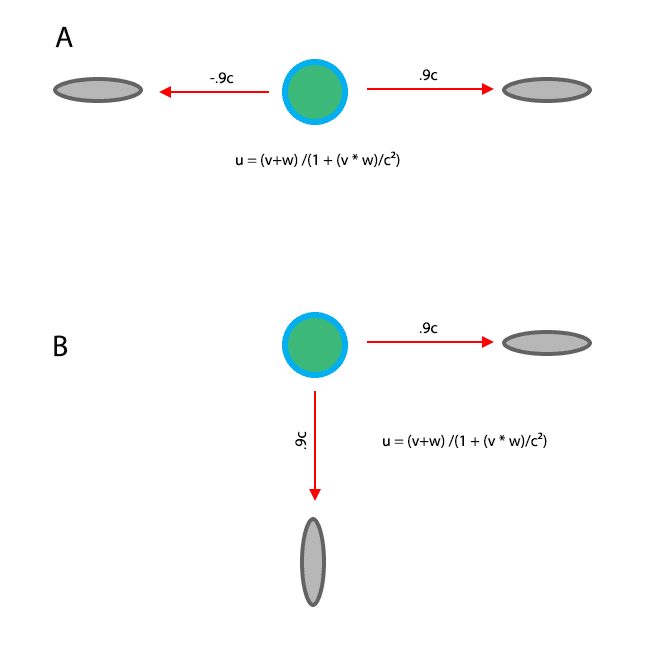
Scenario A:
Two ships are each receding from Earth at .9c in opposite directions. Since these are velocities, they should have opposite signs.
That can't be right, since they immediately cancel out in (v+w) to get zero.
Scenario B:
The two ships are receding orthagonally from Earth.
I thought this would be a simple case of finding the hypotenuse, but that leaves me with one number: 1.27 I need two numbers to apply the formula.
Where am I going wrong?
Scenario A:
Two ships are each receding from Earth at .9c in opposite directions. Since these are velocities, they should have opposite signs.
That can't be right, since they immediately cancel out in (v+w) to get zero.
Scenario B:
The two ships are receding orthagonally from Earth.
I thought this would be a simple case of finding the hypotenuse, but that leaves me with one number: 1.27 I need two numbers to apply the formula.
Where am I going wrong?
