Uncertainty Propagation in Coupled Oscillator

[HermitianField]

I am a senior physics and mathematics major, and this is my last semester. As a result, I am taking advanced physics lab, which feels more like a grad school experiment than an undergrad. One of the labs deals with the modal analysis of three spring-mass systems placed vertically as shown in the picture. The masses and spring constants are similar.

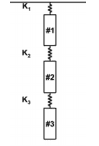
I first measure the spring constant for each spring. I then take the mean of their values and uncertainties to have one spring constant. Thus, I get something of the form \bar{k} \pm \bar{\sigma}. By using kinematics and Newton's second law, I can use the eigenvalue problem to write everything down more conveniently such that we have:

\begin{equation}
\begin{pmatrix}
\frac{-k_{1}-k_{2}}{m_{1}} & \frac{k_{2}}{m_{1}} & 0 \\
\frac{k_{2}}{m_{2}} & \frac{-k_{2}-k_{3}}{m_{2}} & \frac{k_{3}}{m_{2}} \\
0 & \frac{k_{3}}{m_{3}} & \frac{-k_{3}}{m_{3}}
\end{pmatrix}
\begin{pmatrix}
x_{1} \\ x_{2} \\ x_{3}
\end{pmatrix}
= - \omega^{2}\begin{pmatrix}
x_{1} \\ x_{2} \\ x_{3}
\end{pmatrix}
\end{equation}

I then set all k values and their uncertainties to \bar{k} \pm \bar{\sigma}.

My main problem is doing the error propagation for the matrix since I also have an uncertainty to deal with. Clearly, I must end up with three different eigenvalues/eigenfrequencies that have a value and an uncertainty, but I don't know how to do the error propagation at all. I am stuck badly and, while I have two weeks to turn in my report, I would like to have all the error propagation finished ASAP.

 

[jfizzix]

My main problem is doing the error propagation for the matrix since I also have an uncertainty to deal with. Clearly, I must end up with three different eigenvalues/eigenfrequencies that have a value and an uncertainty, but I don't know how to do the error propagation at all. I am stuck badly and, while I have two weeks to turn in my report, I would like to have all the error propagation finished ASAP.

If you know how to solve the eigenvalue equation, you can get formulas for the eigenfrequencies as a function of the spring constants. Then, you can use ordinary error propagation to obtain the uncertainties of the eigenfrequencies in terms of the values and uncertainties of the spring constants. For example:

Where
[itex]\omega_{1}=\omega_{1}(k_{1},k_{2},k_{3})[/itex],
propagation of uncertainty gives us:
[itex]\sigma^{2}(\omega_{1})=\Big(\frac{\partial \omega_{1}}{\partial k_{1}}\Big)^{2}\sigma^{2}(k_{1}) + \Big(\frac{\partial \omega_{1}}{\partial k_{2}}\Big)^{2}\sigma^{2}(k_{2}) + \Big(\frac{\partial \omega_{1}}{\partial k_{3}}\Big)^{2}\sigma^{2}(k_{3})[/itex]
Note that the partial derivatives are evaluated at the respective mean values of [itex](k_{1},k_{2},k_{3})[/itex].

Once this calculation is done, you can let [itex]k_{1}=k_{2}=k_{3}=\bar{k}[/itex] and let [itex]\sigma(k_{1})=\sigma(k_{2})=\sigma(k_{3})=\sigma[/itex] to simplify your final result.

 

[HermitianField]

So you are saying that $$\omega _{1}(k_{1}, k_{2}, k_{3}) = \sqrt{\frac{k_{1}}{m}} + \sqrt{\frac{k_{2}}{m}} + \sqrt{\frac{k_{3}}{m}}$$, right? Again, I assume that $$m_{1} = m_{2} = m_{3} = m$$. I also solved for the eigenvalue problem through MatLab, so I think your formula works only if I solve the eigenvalue problem analytically as opposed to numerically.
If that is true, then what is $$\omega_{2}$$ and $$\omega_{3}$$ ?

 

[jfizzix]

So you are saying that $$\omega _{1}(k_{1}, k_{2}, k_{3}) = \sqrt{\frac{k_{1}}{m}} + \sqrt{\frac{k_{2}}{m}} + \sqrt{\frac{k_{3}}{m}}$$, right?

If that is true, then what is $$\omega_{2}$$ and $$\omega_{3}$$ ?

To find formulas for [itex]\omega_{1}, \omega_{2}, \omega_{3}[/itex], you have to solve the eigenvalue equation given by the matrix in your first post. There should be 3 solutions to the equation (though some may be identical). Since this is a homework problem, I can't do that for you, but I can point out that you may have made a typo in your matrix, since it needs to be symmetric (i.e., equal to its own transpose).

 

[HermitianField]

To find formulas for [itex]\omega_{1}, \omega_{2}, \omega_{3}[/itex], you have to solve the eigenvalue equation given by the matrix in your first post. There should be 3 solutions to the equation (though some may be identical). Since this is a homework problem, I can't do that for you, but I can point out that you may have made a typo in your matrix, since it needs to be symmetric (i.e., equal to its own transpose).

By setting all masses equal to each other, the matrix is symmetric, which is what I did.

 

[HermitianField]

To find formulas for [itex]\omega_{1}, \omega_{2}, \omega_{3}[/itex], you have to solve the eigenvalue equation given by the matrix in your first post. There should be 3 solutions to the equation (though some may be identical). Since this is a homework problem, I can't do that for you, but I can point out that you may have made a typo in your matrix, since it needs to be symmetric (i.e., equal to its own transpose).

I found [itex]\omega_{1}, \omega_{2}, \omega_{3}[/itex] through a nifty WolframAlpha widget. I set x=k1, y=k2, and z=k3. As you can see from the equation of just one eigenvalue, I don't think that is easily differentiated. Is this the only correct way to do uncertainty propagation? If yes, what software can I use to derive these nasty eigenvalue equations?

 

[jfizzix]

I found [itex]\omega_{1}, \omega_{2}, \omega_{3}[/itex] through a nifty WolframAlpha widget. I set x=k1, y=k2, and z=k3. As you can see from the equation of just one eigenvalue, I don't think that is easily differentiated. Is this the only correct way to do uncertainty propagation? If yes, what software can I use to derive these nasty eigenvalue equations?

View attachment 113623

If you're just looking to estimate the uncertainty, and you have experimental values for [itex](k_1,k_2,k_3)[/itex] and for their uncertainties, you can plug in the 8 combinations of values [itex](k_1\pm \sigma_1,k_2\pm\sigma_2,k_3\pm\sigma_3)[/itex] into [itex]\omega_1(k_1,k_2,k_3)[/itex] and see what range of values [itex]\omega_{1}[/itex] takes to estimate its uncertainty.

To do standard error propagation of a function of this complexity, I would use wolfram mathematica, though it's not as difficult to derive as it looks (it's just polynomials, roots, and quotients). It's just a lot to keep track of.

 

[HermitianField]

If you're just looking to estimate the uncertainty, and you have experimental values for [itex](k_1,k_2,k_3)[/itex] and for their uncertainties, you can plug in the 8 combinations of values [itex](k_1\pm \sigma_1,k_2\pm\sigma_2,k_3\pm\sigma_3)[/itex] into [itex]\omega_1(k_1,k_2,k_3)[/itex] and see what range of values [itex]\omega_{1}[/itex] takes to estimate its uncertainty.

To do standard error propagation of a function of this complexity, I would use wolfram mathematica, though it's not as difficult to derive as it looks (it's just polynomials, roots, and quotients). It's just a lot to keep track of.

I was initially thinking of "brute forcing" my experimental values for [itex] (k_{1},k_{2},k_{3})[/itex] as you said. It really does seem like a sufficiently good approximation for the uncertainty. However, I want to be as formal as possible with everything, especially error propagation. It may be the last physics class that I will take, at least for a while. That is why I might just as well show my professors that I truly care about my capstone physics course and give my best shot. Thank you!

 

[HermitianField]

If you're just looking to estimate the uncertainty, and you have experimental values for [itex](k_1,k_2,k_3)[/itex] and for their uncertainties, you can plug in the 8 combinations of values [itex](k_1\pm \sigma_1,k_2\pm\sigma_2,k_3\pm\sigma_3)[/itex] into [itex]\omega_1(k_1,k_2,k_3)[/itex] and see what range of values [itex]\omega_{1}[/itex] takes to estimate its uncertainty.

To do standard error propagation of a function of this complexity, I would use wolfram mathematica, though it's not as difficult to derive as it looks (it's just polynomials, roots, and quotients). It's just a lot to keep track of.

One last thing. Since some of the eigenvalues have complex parts, should I just take the real part of the function [itex] Re(\omega_{2})[/itex] and proceed with the usual standard error propagation?

 

[jfizzix]

One last thing. Since some of the eigenvalues have complex parts, should I just take the real part of the function [itex] Re(\omega_{2})[/itex] and proceed with the usual standard error propagation?

Since the initial matrix is symmetric and real valued, your eigenvalues should be entirely real as well. This is a fundamental property of such matrices, so I would check your calculations if you're getting nonzero values for the imaginary part of the eigenvalues.