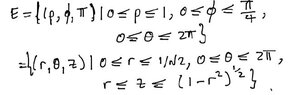- #1
batch3
- 6
- 0
Hi all,
I'm not sure how to get the boundaries in terms of both the spherical and cylindrical coordinates for this question.
View attachment 2504
Here are the boundaries we were given in the solution.
View attachment 2505
How was \(\displaystyle \frac{\pi}{4}\) for φ and \(\displaystyle \frac{1}{\sqrt{2}}\) for r obtained?
Thanks!
I'm not sure how to get the boundaries in terms of both the spherical and cylindrical coordinates for this question.
View attachment 2504
Here are the boundaries we were given in the solution.
View attachment 2505
How was \(\displaystyle \frac{\pi}{4}\) for φ and \(\displaystyle \frac{1}{\sqrt{2}}\) for r obtained?
Thanks!