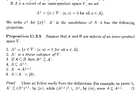The Annihilator of a Set .... Yet Another Question .... Garling, Proposition 11.3.5 - 5 ....

[Math Amateur]

I am reading D. J. H. Garling's book: "A Course in Mathematical Analysis: Volume II: Metric and Topological Spaces, Functions of a Vector Variable" ... ...

I am focused on Chapter 11: Metric Spaces and Normed Spaces ... ...

I need some help in order to understand Garling's proof of Proposition 11.3.5 - 5 ...

Garling's statement and proof of Proposition 11.3.5 reads as follows:View attachment 8965I can follow Garling's proof of Proposition 11.3.5 - 5 (except that when he refers to (iii) and (iv) ... he means 3 and 4 ...)

... ... BUT ... the proof assumes \(\displaystyle (A^{ \bot } )^{ \bot \bot } = (A^{ \bot \bot } )^{ \bot } = A^{ \bot \bot \bot }\) ... ...How do we know that this is the case ... that is, true ... ?

Peter

 

[Olinguito]

... ... BUT ... the proof assumes \(\displaystyle (A^{ \bot } )^{ \bot \bot } = (A^{ \bot \bot } )^{ \bot } = A^{ \bot \bot \bot }\) ... ...

$A^{\bot\bot\bot}$ is just a shorthand way of writing $(A^{ \bot } )^{ \bot \bot }$ or $(A^{ \bot \bot } )^{ \bot}$ – if both are equal. And they are, being equal to $A^\bot$.

 

[Opalg]

the proof assumes \(\displaystyle (A^{ \bot } )^{ \bot \bot } = (A^{ \bot \bot } )^{ \bot } = A^{ \bot \bot \bot }\) ... ...How do we know that this is the case ... that is, true ... ?

To see that the annihilator operation is associative, notice that the condition for $x\in (A^\bot)^{\bot\bot}$ is the same as the condition for $x\in(A^{\bot\bot})^\bot$. In both cases, the condition is that $\langle x,y\rangle = 0$ for all $y$ in $A^{\bot\bot}$.