- #1
Math Amateur
Gold Member
MHB
- 3,998
- 48
I am reading Anthony W. Knapp's book: Basic Algebra in order to understand tensor products ... ...
I need some help with a further aspect of the proof of Theorem 6.10 in Section 6 of Chapter VI: Multilinear Algebra ...
The text of Theorem 6.10 reads as follows:

 The above proof mentions Figure 6.1 which is provided below ... as follows:
The above proof mentions Figure 6.1 which is provided below ... as follows:
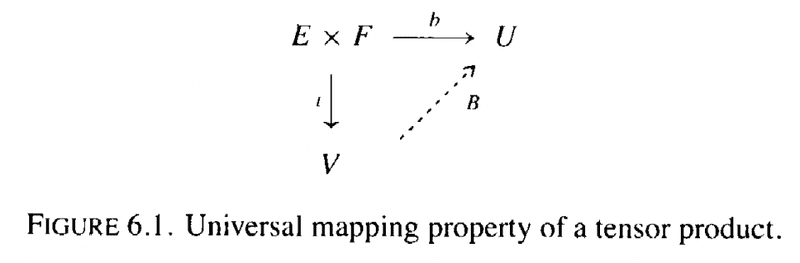
In the above text, in the proof of Theorem 6.10 under "PROOF OF EXISTENCE" we read:
" ... ... The bilinearity of [itex]b[/itex] shows that [itex]B_1[/itex] maps [itex]V_0[/itex] to [itex]0[/itex]. By Proposition 2.25, [itex]B_1[/itex] descends to a linear map [itex]B \ : \ V_1/V_0 \longrightarrow U[/itex], and we have [itex]Bi = b[/itex]. "
My questions are as follows:Question 1
Can someone please give a detailed demonstration of how the bilinearity of [itex]b[/itex] shows that [itex]B_1[/itex] maps [itex]V_0[/itex] to [itex]0[/itex]?Question 2
Can someone please explain what is meant by "[itex]B_1[/itex] descends to a linear map [itex]B \ : \ V_1/V_0 \longrightarrow U[/itex]" and show why this is the case ... also showing why/how [itex]Bi = b[/itex] ... ... ?
Hope someone can help ...
Peter===========================================================*** EDIT ***
The above post mentions Proposition 2.25 so I am providing the text ... as follows:

============================================================*** EDIT 2 ***
After a little reflection it appears that the answer to my Question 2 above should "fall out" or result from matching the situation in Theorem 6.10 to that in Proposition 2.25 ... also I have noticed a remark of Knapp's following the statement of Proposition 2.25 which reads as follows:
 So that explains the language: "[itex]B_1[/itex] descends to a linear map [itex]B \ : \ V_1/V_0 \longrightarrow U[/itex]" ... ...
So that explains the language: "[itex]B_1[/itex] descends to a linear map [itex]B \ : \ V_1/V_0 \longrightarrow U[/itex]" ... ...
BUT ... I remain perplexed over question 1 ...
Peter
I need some help with a further aspect of the proof of Theorem 6.10 in Section 6 of Chapter VI: Multilinear Algebra ...
The text of Theorem 6.10 reads as follows:
In the above text, in the proof of Theorem 6.10 under "PROOF OF EXISTENCE" we read:
" ... ... The bilinearity of [itex]b[/itex] shows that [itex]B_1[/itex] maps [itex]V_0[/itex] to [itex]0[/itex]. By Proposition 2.25, [itex]B_1[/itex] descends to a linear map [itex]B \ : \ V_1/V_0 \longrightarrow U[/itex], and we have [itex]Bi = b[/itex]. "
My questions are as follows:Question 1
Can someone please give a detailed demonstration of how the bilinearity of [itex]b[/itex] shows that [itex]B_1[/itex] maps [itex]V_0[/itex] to [itex]0[/itex]?Question 2
Can someone please explain what is meant by "[itex]B_1[/itex] descends to a linear map [itex]B \ : \ V_1/V_0 \longrightarrow U[/itex]" and show why this is the case ... also showing why/how [itex]Bi = b[/itex] ... ... ?
Hope someone can help ...
Peter===========================================================*** EDIT ***
The above post mentions Proposition 2.25 so I am providing the text ... as follows:
============================================================*** EDIT 2 ***
After a little reflection it appears that the answer to my Question 2 above should "fall out" or result from matching the situation in Theorem 6.10 to that in Proposition 2.25 ... also I have noticed a remark of Knapp's following the statement of Proposition 2.25 which reads as follows:
BUT ... I remain perplexed over question 1 ...
Peter
Attachments
Last edited:


