String theory - no-ghost state - virasoro constraints

[binbagsss]

1. Homework Statement

Question (with the following definitions here):

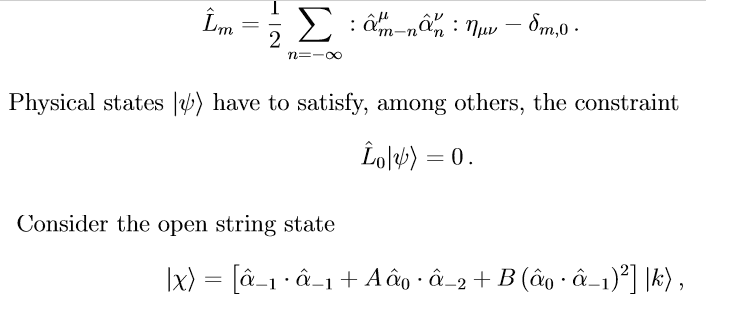
- Consider ##L_0|x>=0## to show that ##m^2=\frac{1}{\alpha'}##
- Consider ##L_1|x>=0 ## to conclude that ## 1+A-2B=0##

- where ##d## is the dimension of the space ##d=\eta^{uv}\eta_{uv}##

For the L1 operator I am able to get the correct expression of ##1+A-2B=0##
I am struggling with L0

Any help much appreciated.2. Homework Equations

##\alpha^u_0={p^u}\sqrt{2 \alpha'}##

##\alpha_{n>0}## annihilate

##\alpha_{n<0}## create

## [\alpha_n^u, \alpha_m^v]=n\delta_{n+m}\eta^{uv}## (*)

where ##\eta^{uv}## is the Minkowski metric

##p^u|k>=k^u|k>##3. The Attempt at a Solution Here is my L0 attempt- Consider ##L_0 |x>=0## to show that ##m^{2}=1/\alpha'##

##L_0=(\alpha_0^2+2\sum\limits_{n=1}\alpha_{-n}\alpha_{n}-1)##

So first of all looking at the first term of ##|x>## I need to consider:

##L_0 \alpha_{-1}\alpha_{-1}|k> =(\alpha_0^2+2\alpha_{-1}\alpha_{1}-1)\alpha_{-1}\alpha_{-1}##

Considering the four product operator and using the commutators in the same way as done for ##L_1## I get from this:

##L_0\alpha_{-1}\alpha_{-1}|k> =(\alpha_0^2+4-1)\alpha_{-1}\alpha_{-1}|k>## (**)

Here's how I got it:(dropped indices in places, but just to give idea, ##\eta^{uv}## the minkowksi metric)
##2\alpha_{-1}\alpha_{1}\alpha_{-1}\alpha_{-1} |k>
= 2(\alpha_{-1}(\alpha_{-1}\alpha_1+\eta)\alpha_{-1})|k>
= 2(\alpha_{-1}\alpha_{-1}\alpha_1\alpha_{-1}+\eta\alpha_{-1}\alpha_{-1})|k>
= 2(\alpha_{-1}\alpha_{-1}(\alpha_{-1}\alpha_{1}+\eta)+\eta\alpha_{-1}\alpha_{-1})|k>
=2(\alpha_{-1}\alpha_{-1}(0+\eta|k>)+\eta\alpha_{-1}\alpha_{-1}|k>)
= 2(2\alpha_{-1}.\alpha_{-1})##

so from (**) I have:

##L_0\alpha_{-1}\alpha_{-1}|k> =(\alpha_0^2+3)\alpha_{-1}\alpha_{-1}|k>=0##
##=(2\alpha'p^2+3)\alpha_{-1}\alpha_{-1}|k>=0##
##\implies 2\alpha'p^2+3=0##
## \implies 2(-m^2)\alpha'=-3##

So I get ## m^{2}=3/\alpha'## and not ##1/\alpha'## :(

Any help much appreciated ( I see the mass is independent of ##A## and ##B## so I thought I'd deal with the first term before confusing my self to see why these terms vanish)

 

[AndyW]

Thank you for sharing your attempt at solving the problem. I appreciate the effort you have put into it. However, I believe there may be a few errors in your calculations.

Firstly, in your first line, you have written ##L_0=\alpha_0^2+2\sum\limits_{n=1}\alpha_{-n}\alpha_{n}-1##. This is incorrect as the correct expression is ##L_0=\alpha_0^2+2\sum\limits_{n=1}\alpha_{-n}\alpha_{n}+1##. The reason for this is that the zero mode term ##\alpha_0^2## should have a positive sign and not a negative sign. Additionally, the constant term in the expression should be a positive one, as we will see in the next steps.

Next, you have used the commutation relation ##[\alpha_n^u, \alpha_m^v]=n\delta_{n+m}\eta^{uv}## to calculate ##L_0 \alpha_{-1}\alpha_{-1}|k>##. However, this relation holds only for ##n, m \neq 0##. For the zero modes, the commutation relation is ##[\alpha_0^u, \alpha_0^v]=\eta^{uv}##. Using this, we can write ##L_0 \alpha_{-1}\alpha_{-1}|k>=(\alpha_0^2+2\alpha_0.\alpha_0+1)\alpha_{-1}\alpha_{-1}|k>##.

Now, using the definition of the zero mode operators and the momentum operator, we can write ##p^u|k>=k^u|k> \implies \alpha_0^u|k>=k^u/\sqrt{2\alpha'}|k>##. Substituting this in the above expression, we get ##L_0 \alpha_{-1}\alpha_{-1}|k>= (2\alpha'p^2+3)\alpha_{-1}\alpha_{-1}|k>##. Now, using the fact that ##\alpha_{-1}\alpha_{-1}|k>=0##, we get ##L_0 \alpha_{-1}\alpha_{-1}|k>=0##.

Therefore, we have