Solving the Friction Force Puzzle: Range of Acceleration for Slab

[Beamsbox]

I just realized I don't even have to do this problem, but I've thought too much about it, and at times like this I tend to be a bit OCD.

If someone could just get me started on the right track of thought that would be great!

Q:
In figure:

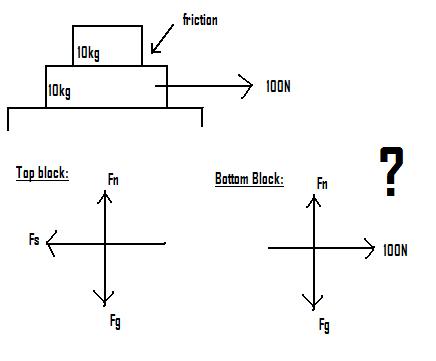
(http://i51.photobucket.com/albums/f362/BeamsBox/PhysicsBlocks.jpg)

a horizontal force of 100N is to be applied to a 10kg slab that is initially stationary on a frictionless floor, to accelerate the slab. A 10kg block lies on top of the slab; the coefficient of friction (mue) between the block and the slab is not known, and the block might slip.
A) Considering the possibility, wha tis the possible range of values for the magnitude of the slab's acceleration a_slab? (Hint: You don't need written calculations; just consider extreme values for (mue).)

My thoughts:
First, the force of friction between the slab and the block,
F_s(max) = (mue)F_N, and
F_N = mg.
So,
F_s(max) = (mue)(mg)

Now, noting this relation, it makes sense to me that F_s(max) cannot be greater than F_N... but this could also be wrong, because it's not that it can't be greater than F_N, it just can't be greater than F_N times (mue)... which is unknown... that's where I lose myself.

I just don't know what I need to consider, that I'm obviously not...


;)

 

[hikaru1221]

My thoughts:
First, the force of friction between the slab and the block,
F_s(max) = (mue)F_N, and
F_N = mg.
So,
F_s(max) = (mue)(mg)

Now, noting this relation, it makes sense to me that F_s(max) cannot be greater than F_N... but this could also be wrong,

Edit: Sorry, misread it. Anyway, look at the bold equation, they're equal.

Edit 2: Oh I see your problem now.
Don't pay attention to equations above. Just think: What are the extreme cases for the motion of the slab and the block? What if the friction is too small? What if it is too great?

 

[Beamsbox]

I see that they're equal... but (mue) is an unknown, multiplied by the normal force... so they're not equal, unless you take into account the unknown coefficient... not sure where you're leading me...

 

[hikaru1221]

No, I mean [tex]F_{smax}[/tex] and [tex]\mu F_N[/tex] are equal, so what's the point of comparing [tex]F_{smax}[/tex] and [tex]F_N[/tex]? What is with that "they're equal" and then "so they're not equal"?

Now back to the main question. The problem asks for the acceleration of the slab. And what the hint means is that you must think of the extreme scenarios, imagine what happens in those scenarios and don't write down anything. Those are:
1 - When the friction is so small that it can be ignored.
2 - When the friction is so great.
Each extreme case will correspond to a relative motion between the slab and the block.

 

[Beamsbox]

No, I mean [tex]F_{smax}[/tex] and [tex]\mu F_N[/tex] are equal, so what's the point of comparing [tex]F_{smax}[/tex] and [tex]F_N[/tex]? What is with that "they're equal" and then "so they're not equal"?

Now back to the main question. The problem asks for the acceleration of the slab. And what the hint means is that you must think of the extreme scenarios, imagine what happens in those scenarios and don't write down anything. Those are:
1 - When the friction is so small that it can be ignored.
2 - When the friction is so great.
Each extreme case will correspond to a relative motion between the slab and the block.

Okay, so when the friction is so small, the max acceleration to keep it from falling off would be zero, because without friction it would just stay there.

And big, this one's a bit more difficult, I think... not sure where the acceleration fits into my brain... I better put this down for the night. Thanks for the help too!

 

[modulus]

FYI: On your diagram, you made the free-body diagram of the bottom block is slightly wrong. The top block will also exert some friction on it (obviously in opposition to the 100N force). This stems from Newton's Third Law.

Now I think you can work on the second part of the problem more easily: The case of max friction.

Also, keep this in mind; it will clear up your headache when you get stuck in the middle: 'The friction is self-adjustable, i.e., it will change it's value so it can counteract the force on the body.