Solving a Magnetic Problem with Maxwell Equation

[we are the robots]

Hi, I'm very lost in this problem, anyone can help me?
The problem is this:

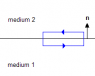
In steady state the magnetic field H satisifes the Maxwell equation delxH=J , where J is the current density (per square meter). At the boundary between two media there is a surface current density K (perimeter). Show that a boundary contidion on H is
nx(H2-H1)=K.
n is a unit vector normal to the surface and out of medium 1.
Hint: consider a narrow loop perpendicular to the interface as shown in the figure. (The figure is attached).

Note: del x H is the curl of H.
Any ideas?
Thank you.

 

[Bonfield]

The hint is a good one.

First integrate and then apply Stokes theorem to your curl H = J equation to get the equivalent integral form. You will have a line integral of H around a closed curve, which you should make your rectangular loop. The other side of the equation will have the total current flowing through the loop, which is related to K. Set this up carefully, and you will have the result you want.

 

[Graeme Robinson]

Hi there,

Firstly, don't worry if you're feeling lost in this problem. Magnetism and Maxwell's equations can be quite complex and it's normal to struggle with them. Let's break down the problem and see if we can come up with a solution.

The first thing we need to do is understand the given information. We are told that we have a steady state magnetic field, which means that the field is not changing over time. We also know that the magnetic field H satisfies the Maxwell equation del x H = J, where J is the current density. This means that the curl of the magnetic field is equal to the current density.

Now, we are given a boundary between two media, and we are told that there is a surface current density K at this boundary. Our task is to show that the boundary condition on H is nx(H2-H1)=K, where n is a unit vector normal to the surface and out of medium 1.

To solve this problem, we need to use the hint given to us. The hint tells us to consider a narrow loop perpendicular to the interface, as shown in the attached figure. This loop will have a small area, and we can use it to apply Ampere's law, which states that the line integral of the magnetic field around a closed loop is equal to the current passing through the loop.

Now, if we consider the loop at the boundary between the two media, we can see that the current passing through the loop is equal to the surface current density K. This is because the loop is perpendicular to the interface, so all of the current passing through it is also passing through the interface.

Using Ampere's law, we can write the following equation:

∮H⋅dl = K

The left-hand side of this equation is the line integral of the magnetic field around the loop, which can also be written as the surface integral of the curl of the magnetic field (using Stokes' theorem). So, we can rewrite the equation as:

∬(del x H)⋅dS = K

Now, we know from the Maxwell equation given in the problem that del x H = J. So, we can substitute this into the equation to get:

∬J⋅dS = K

We can also rewrite the surface integral on the left-hand side as the integral of the current density over the surface, which gives us:

∫J⋅d