Solve coupled nonlinear differential equations

[eahaidar]

Good evening I have these coupled equations and was wondering if there is any chance solving them analytically. If not, how would you approach it numerically? (shown in attachment)
Thank you very much

 

[BvU]

Hello eahaidar,

Don't you think that is a bit terse ? Some explanation of the variables might be in order. Complex variables ? Probably: in particular: g -- if g is real nothing happens.

Below is the homework template; you case may not be a homework exercise, but the systematic approach might be useful anyway !

1. The problem statement, all variables and given/known data

2. Homework Equations

3. The Attempt at a Solution​

 

[eahaidar]

Hello eahaidar,

Don't you think that is a bit terse ? Some explanation of the variables might be in order. Complex variables ? Probably: in particular: g -- if g is real nothing happens.

Below is the homework template; you case may not be a homework exercise, but the systematic approach might be useful anyway !

1. The problem statement, all variables and given/known data

2. Homework Equations

3. The Attempt at a Solution​

Thank you for your time. The variables are [/0], [/STOKES], and [/SBS]. As for g, it is a real constant number despite having many variables.
My attempt well: i only could find a relation between the 3 equations. Clearly equation 1 = 2 + 3 however other than the initial conditions of [/STOKES] and [/SBS] are available while [/0] is found at the end of the length of a waveguide L. I do not know what to do next.
Hopefully you can help me out

 

[BvU]

If ##\ g\ ## is a real number (but a function of many non-involved variables, but not ##z,\ I_0, I_{SBS} {\rm \ or \ } I_{stokes}\ ## -- correct ? ), then what does ##Im(g)## mean ?

I also have difficulty understanding your "Clearly equation 1 = 2 + 3 " since that implies ##\ \left | A_0 \right |^2 = 1 \ ##, which I haven't seen in the problem description ?

Whatever, my first approach would be a Runge-Kutta integration and use a shooting method to end up with ##Cst_1## and ##Cst_2## -- which are given constants at ##z = L## -- but then it seems you intend to go the other way with initial conditions for ##\ I_{SBS} {\rm \ and \ } I_{stokes}\ ## at ##\,z = L\,## (?) and have ##\ I_0(0) \ ## at the end of the pipe ?

--

 

[eahaidar]

Thank you for your time. g is complex and I apologize for that. However, Im(g) is a constant number since it varies with another variable other than z. So let's say Im(g)= 0.5
What I meant from 1=2 +3 is that notice that d(I0) /dz = d( ISBS)/dz + d(I STOKES)/dz.
As for your approach, I0 represents the intensity of light introduced into the medium while SBS and STOKES represent 2 light waves counter propagating the forward wave of index 0 which puts me in trouble since initally at z=0 I only have the forward wave.
With that being said, is your suggestion still valid? If not what other choice do I have?

 

[BvU]

What I meant from 1=2 +3 is that notice that d(I0) /dz = d( ISBS)/dz + d(I STOKES)/dz.

I still see an ##|A_0|^2## sitting there. is it constant and equal to 1 ? But even d(I0) /dz = (d( ISBS)/dz)/A₀² + d(I STOKES)/dz is enough to reduce this to a two differential equations problem -- doesn't change the suggestion.

But it is a bit strange that sbs and stokes should both end up at Cst1 for z=L

 

[eahaidar]

Now i see your point. Drop the |A0|^2 since it is inside I0.
Now what i claimed that first equation is the sum of second and third. SBS and Stokes should be propagate on the other side of the medium and therefore there are initially at z=L that means they are introduced at the end of the medium. Does that make any sense or change anything?

 

[BvU]

SBS and STOKES represent 2 light waves counter propagating the forward wave of index 0 which puts me in trouble since initally at z=0 I only have the forward wave

So is this a set of differential equations in z only, or is there some time dependence that plays a role too ?

So far "Initial conditions" to me meant conditions at z = 0 and "boundary conditions" meant conditions at z = L

Are you doing things like Y Zhu describes in his thesis (e.g. (2.27) ) ? (stumbled on it while trying to decipher the term SBS)

 

[eahaidar]

Yes it only relies on z.
SBS stands for stimulated Brillouin scattering and so far yes the initial conditions are as you mentioned

 

[BvU]

So, if I summarize: you want to solve
$$ \begin{cases}
{dI_0\over dz} & = \ \ \ \ Im(g) I_0(I_{sbs}-I_{stokes})\\ {dI_{sbs}\over dz} &=\ \ \ \ Im(g) I_0 I_{sbs}\\ {dI_{stokes}\over dz} &= - Im(g) I_0 I_{stokes}
\end{cases}
$$ With initial condition ##\ I_0(0) = C_2,\ ## and boundary conditions ##\ I_{sbs} (L) = I_{stokes}(L) = C_1##

Since 1 = 2 + 3 ## {d\over dz}( I_0 - I_{sbs}-I_{stokes}) = 0 \Rightarrow I_0 - I_{sbs}-I_{stokes} = Const ##, an unknown constant

I leave out the Im(g) (It's an over-all scale factor ) and give it to an integrator with initial conditions C2, u and v, respectively. Then I fumble with u and v until both end up at ##C_1##. In the picture below ##C_2 = 0.1, \ \ C_1 = 0.0312## u and v come out 0.0135, 0.072

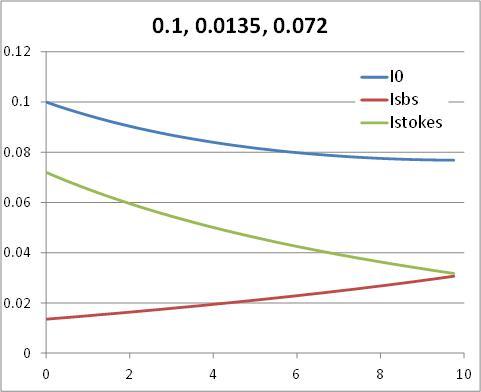
I did the fumbling (shooting) by hand, but you can let the computer do it.Since 1 = 2 + 3, ## \ \ {d\over dz}( I_0 - I_{sbs}-I_{stokes}) = 0 \ \ \Rightarrow \ \ I_0 - I_{sbs}-I_{stokes} = Const ##, an unknown constant, you don't really have to integrate all three (##Const = C_2 - u - v## )

No joy finding something analytical (lack of talent for that kind of thing ..).

--

 

[eahaidar]

Very interesting my friend. How did you get the plots? What program did you use?
I know analytical stuff is hard but they come into handy. Another condition i found was that ISBS * I Stokes = CST if you divide equation 2 from 3.
I am not sure how you got the curves to be honest. Is is just fumbling with the numbers or what exactly?
I really want to thank you for your help

 

[BvU]

(Sorry, I missed this alert during the weekend).
Program is a dynamic simulation program for the chemical industry, called aspen custom modeler. But all I use is the integrator, so I didn't mention it. It has lousy graphics, so picture is made by moving the data to excel. Also easier to do further analysis: take logarithm, fit that to a polynomial, to see if it's a simple exponential. It is not:
(##\ \ln(I_{\rm stokes} ) = -2.6356 - 0.0939 z + 0.0011 z^2\ ## )

Got the curves by doing the forward integration from z = 0 to 10. Chose C₂ = I₀(0) = 0.1 and played around with I_SBS(0) and I_stokes(0) until they ended up at the same value. I called that C₁. Normally you would let the computer do the guessing (shooting method) with a reasonable efficiency.

So still no joy finding something analytical.

What tools do you have at your disposal for this ?

--

 

[eahaidar]

(Sorry, I missed this alert during the weekend).
Program is a dynamic simulation program for the chemical industry, called aspen custom modeler. But all I use is the integrator, so I didn't mention it. It has lousy graphics, so picture is made by moving the data to excel. Also easier to do further analysis: take logarithm, fit that to a polynomial, to see if it's a simple exponential. It is not:
(##\ \ln(I_{\rm stokes} ) = -2.6356 - 0.0939 z + 0.0011 z^2\ ## )

Got the curves by doing the forward integration from z = 0 to 10. Chose C₂ = I₀(0) = 0.1 and played around with I_SBS(0) and I_stokes(0) until they ended up at the same value. I called that C₁. Normally you would let the computer do the guessing (shooting method) with a reasonable efficiency.

So still no joy finding something analytical.

What tools do you have at your disposal for this ?
--

I usually use MATLAB for any simulation. I went through the equations. With the help of a colleague, we managed to reduce the coupled equations to a single equation. I will update you on that once i get to the bottom of this equation which includes the 3 variables. Again thanks for your help and would love to learn your integrator. Sounds fun to use.

 

[BvU]

Yes, ACM is fun, but if you already have matlab: there's integrators available by the truckload and they are free. And shooting isn't a problem either! Well documented and built-in too, I see from the nice example on his p. 174.

I understand you are still eager to get an analytical solution (e.g. in the other thread), but I can't really help there.

[edit] I browsed through some earlier posts by eahaidar and found you were already pointed to ode45 in May 2014 ! Any luck getting that to work since then ? I mean, you can do a lot of work numerically and keep an eye open for analytical solution opportunities at the same time !

By the way, did you find anything useful in the Zhu thesis from link in post #8 ?