- #1
gex
- 37
- 2
Homework Statement
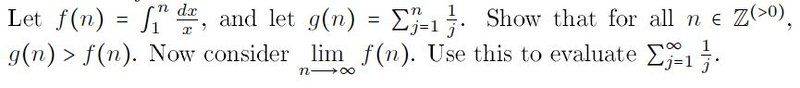
The attempt at a solution
Hi there, in an attempt to prove that g(n) is greater than f(n), I graphed both functions on the same axes and it is visually obvious that g(n) is greater than f(n), but I am not sure how I would go about proving this for all positive integers in a mathematically rigorous way. Any guidance is greatly appreciated.
The attempt at a solution
Hi there, in an attempt to prove that g(n) is greater than f(n), I graphed both functions on the same axes and it is visually obvious that g(n) is greater than f(n), but I am not sure how I would go about proving this for all positive integers in a mathematically rigorous way. Any guidance is greatly appreciated.
