- #1
DuckAmuck
- 236
- 40
I'm basically trying to understand the 2-D case of the catenary cable problem. The 1-D case is pretty straightforward, you have a functional of the shape of a cable with a constraint for length and gravity, and you get the explicit function of the shape of a cable.
But if you imagine a square canvas pinned in 4 places:
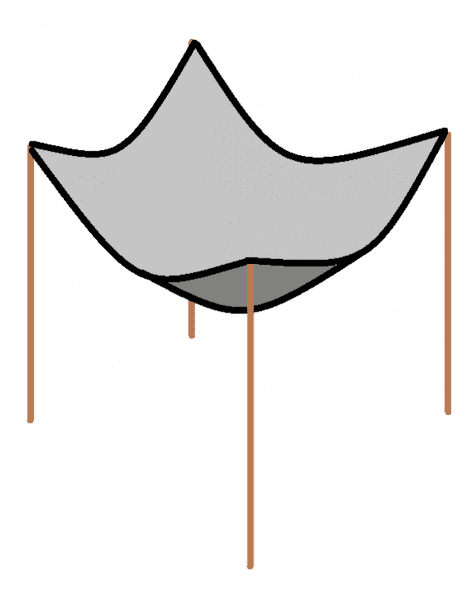
It is not as obvious what the shape is. I'd expect the result to be a product of two catenary shapes, something like: Sheet(x,y) = Cat(x)*Cat(y). I apply a constraint to surface area of the sheet, but get wacky results. Any help will be appreciated. Thanks.
But if you imagine a square canvas pinned in 4 places:
It is not as obvious what the shape is. I'd expect the result to be a product of two catenary shapes, something like: Sheet(x,y) = Cat(x)*Cat(y). I apply a constraint to surface area of the sheet, but get wacky results. Any help will be appreciated. Thanks.