- #1
harpazo
- 208
- 16
Set up an integral for both orders of integration.
DO NOT EVALUATE THE INTEGRAL.
Let S S = double integrals
Let R = region
S S (x^2 + y^2) dA
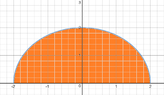
R: semicircle bounded by y = {4 - x^2}, y = 0
I can graph the region but have no idea how to proceed from there. I need solution steps.
DO NOT EVALUATE THE INTEGRAL.
Let S S = double integrals
Let R = region
S S (x^2 + y^2) dA
R: semicircle bounded by y = {4 - x^2}, y = 0
I can graph the region but have no idea how to proceed from there. I need solution steps.