Resolving Velocity Components in Constrained Motion

[decentfellow]

I have been having some problem resolving the velocity component along the rope. My question will be clear if you read an illustration that I encountered which is very helpful in showing my doubt very clearly.

In the Fig. given below the block ##'A'## and ##'B'## are connected with an in-extensible string. The block ##'A'## can slide on a smooth horizontal surface.

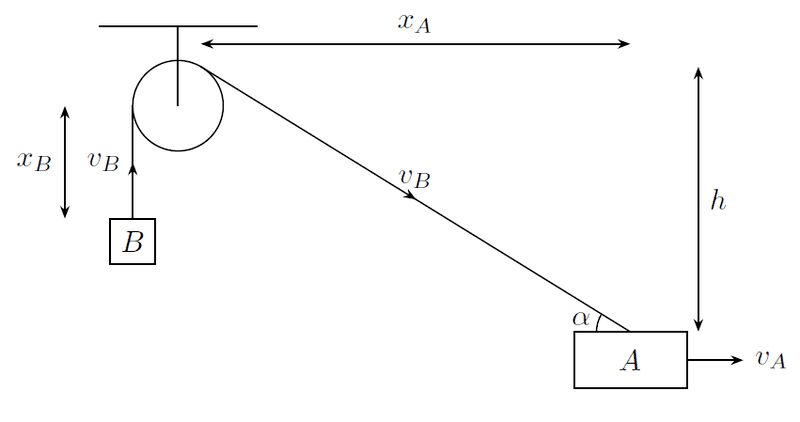
My approaches to form the kinematics constraint equations:-

Approach 1:-
The length ##\ell## of the string connecting the two blocks ##A## and ##B## can be written as follows
$$\sqrt{{x_A}^2+h^2}+x_B+R\theta=\ell$$
On differentiating the above equation we get
$$\dfrac{x_A}{\sqrt{{x_A}^2+h^2}}\cdot\dfrac{dx_A}{dt}+\dfrac{dx_B}{dt}=0\implies \dfrac{x_A}{\sqrt{{x_A}^2+h^2}}\cdot\dfrac{dx_A}{dt}=-\dfrac{dx_B}{dt}$$
As the block ##A## moves rightward ##x_A## increases while ##x_B## decreases. So, ##\dfrac{dx_A}{dt}=v_A## and ##\dfrac{dx_B}{dt}=-v_B##. So, the kinematic constraint equation for velocity is as follows
$$\dfrac{x_A}{\sqrt{{x_A}^2+h^2}}\cdot v_A=v_B\implies v_A\cos\alpha=v_B\ \qquad\qquad\left(\because \cos\alpha=\dfrac{x_A}{\sqrt{{x_A}^2+h^2}}\right)$$

Approach 2:-

The velocity of block ##B##, ##v_B## is along the string hence there could be two possible constraints according to me as follows:-
$$v_B\sec\alpha=v_A$$
or
$$v_B\cos\alpha=v_A$$
Please do tell me as why ##v_B\sec\alpha=v_A## is correct and the other one is wrong.

I had considered that what would have happened if the velocities in both the cases (the cases being the projection of the velocity along the rope in the direction of the movement of block ##A##, and the other one being the projection of the velocity of the block ##A## along the direction of the rope) if resolved into components would affect the movement of the one, in the direction of which the velocities have been resolved.

Case 1:-

So, what I had considered in the case of the velocity along the rope being projected in the direction of the notion of the block ##A## is as follows:-

If the velocity of the rope is resolved as stated above then, in the direction of the motion of the block ##A## the projected velocity will be ##v_B\cos\alpha## and in the perpendicular direction it will be ##v_B\sin\alpha##, as the block is not allowed to move in that direction, so the ground does something(yeah, the ground does something, I am not at all sure if the ground does something in this case, so some clarification on this too) which doesn't let it move in the perpendicular direction. So, according to me this is a probable case too.

Case 2:-

In this case what I had considered was that if we resolve the velocity of the block ##A## along the rope and perpendicular to the rope we get that the velocity component along the rope comes out to be ##v_A\cos\alpha## and perpendicular to it comes out to be ##v_A\sin\alpha##. Now, the perpendicular component changes the direction of the rope and the component along the rope produces the needed velocity along the rope to make the block ##B## move upwards. So, this case is also possible.

So, what is wrong in the 1st case such that it is not the answer, but the case-2 is.

 

[conscience]

Approach 1:-
The length ##\ell## of the string connecting the two blocks ##A## and ##B## can be written as follows
$$\sqrt{{x_A}^2+h^2}+x_B+R\theta=\ell$$
On differentiating the above equation we get
$$\dfrac{x_A}{\sqrt{{x_A}^2+h^2}}\cdot\dfrac{dx_A}{dt}+\dfrac{dx_B}{dt}=0\implies \dfrac{x_A}{\sqrt{{x_A}^2+h^2}}\cdot\dfrac{dx_A}{dt}=-\dfrac{dx_B}{dt}$$
As the block ##A## moves rightward ##x_A## increases while ##x_B## decreases. So, ##\dfrac{dx_A}{dt}=v_A## and ##\dfrac{dx_B}{dt}=-v_B##. So, the kinematic constraint equation for velocity is as follows
$$\dfrac{x_A}{\sqrt{{x_A}^2+h^2}}\cdot v_A=v_B\implies v_A\cos\alpha=v_B\ \qquad\qquad\left(\because \cos\alpha=\dfrac{x_A}{\sqrt{{x_A}^2+h^2}}\right)$$

Correct .

Approach 2:-

The velocity of block ##B##, ##v_B## is along the string hence there could be two possible constraints according to me as follows:-
$$v_B\sec\alpha=v_A$$
or
$$v_B\cos\alpha=v_A$$
Please do tell me as why ##v_B\sec\alpha=v_A## is correct and the other one is wrong.

Because you need component of velocity of the blocks along the string not the other way round . The component of velocity of string along the direction of motion of blocks are not equal .

I had considered that what would have happened if the velocities in both the cases (the cases being the projection of the velocity along the rope in the direction of the movement of block ##A##, and the other one being the projection of the velocity of the block ##A## along the direction of the rope) if resolved into components would affect the movement of the one, in the direction of which the velocities have been resolved.

Same reasoning as before .

 

[decentfellow]

Correct .
Because you need component of velocity of the blocks along the string not the other way round . The component of velocity of string along the direction of motion of blocks are not equal .

That's what I wanted to know, that why is it that the velocity of the string is equal to the velocity of the block along the string and that's why I considered two cases that I have written in my first post, and I still can't understand that why is it that "The component of velocity of string along the direction of motion of blocks are not equal".

 

[conscience]

That's what I wanted to know, that why is it that the velocity of the string is equal to the velocity of the block along the string and that's why I considered two cases that I have written in my first post, and I still can't understand that why is it that "The component of velocity of string along the direction of motion of blocks are not equal".

The motion of the right part of string (i.e from pulley to A ) is a combination of rotation around the pulley as well translation parallel to its length .

Your misconception is the belief that the opposite ends of the string must have the same velocities. They don't. Only the component of the motion parallel to the string is constrained. The ends of the string are completely free to move in the direction perpendicular to the string.

The tip of the string connected to block A has velocity equal to that of A . This velocity can be resolved into two components ##v_Acosα## along the length of the string and ##v_Asinα## . ##v_Asinα## is the velocity of the tip of the string connected to A which signifies rotation of this string around the pulley . It is not responsible for increase in length of the string . Only the component ##v_Acosα## is responsible for an increase in the length of the string . Now since the length is constant , hence rate at which the length decreases i.e ##v_B## should be equal to the rate at which length increases i.e ##v_Asinα## .

 

[decentfellow]

The motion of the right part of string (i.e from pulley to A ) is a combination of rotation around the pulley as well translation parallel to its length .

Your misconception is the belief that the opposite ends of the string must have the same velocities. They don't. Only the component of the motion parallel to the string is constrained. The ends of the string are completely free to move in the direction perpendicular to the string.

The tip of the string connected to block A has velocity equal to that of A . This velocity can be resolved into two components ##v_Acosα## along the length of the string and ##v_Asinα## . ##v_Asinα## is the velocity of the tip of the string connected to A which signifies rotation of this string around the pulley . It is not responsible for increase in length of the string . Only the component ##v_Acosα## is responsible for an increase in the length of the string . Now since the length is constant , hence rate at which the length decreases i.e ##v_B## should be equal to the rate at which length increases i.e ##v_Asinα## .

That was a fabulous explanation. Now, it has been cleared as to what was the key reason that made me take the two cases, which was exactly what you have written in your second paragraph and the solution to that in the misconception in the second paragraph. Thanks again for all your time and effort.

 

[tellmesomething]

The motion of the right part of string (i.e from pulley to A ) is a combination of rotation around the pulley as well translation parallel to its length .

Your misconception is the belief that the opposite ends of the string must have the same velocities. They don't. Only the component of the motion parallel to the string is constrained. The ends of the string are completely free to move in the direction perpendicular to the string.

The tip of the string connected to block A has velocity equal to that of A . This velocity can be resolved into two components ##v_Acosα## along the length of the string and ##v_Asinα## . ##v_Asinα## is the velocity of the tip of the string connected to A which signifies rotation of this string around the pulley . It is not responsible for increase in length of the string . Only the component ##v_Acosα## is responsible for an increase in the length of the string . Now since the length is constant , hence rate at which the length decreases i.e ##v_B## should be equal to the rate at which length increases i.e ##v_Asinα## .

What do you mean by the ends of the string are free to move perpendicularly? Aren't the ends are what is connected to the blocks

 

[PeroK]

What do you mean by the ends of the string are free to move perpendicularly? Aren't the ends are what is connected to the blocks

Note that this thread is almost exactly seven years old.