- #1
mysci
- 9
- 0
We know the rule of cross product
Why here |absinΘ| =
Thanks for explanation.
|a||b|sinθ is the area of the base, and is also the magnitude of the cross product of ##\vec{a}## and ##\vec{b}## -- i.e., |##\vec{a}## X ##\vec{b}|##. |c|cosφ gives the height of the parallelipiped. The product of the area of the base and the height gives the volume of the cell.mysci said:View attachment 79881
We know the rule of cross productView attachment 79882 or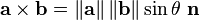
Why here |absinΘ| = View attachment 79883 , and View attachment 79884 = c cos Φ in the above picture?
Mark44 said:|a||b|sinθ is the area of the base, and is also the magnitude of the cross product of ##\vec{a}## and ##\vec{b}## -- i.e., |##\vec{a}## X ##\vec{b}|##. |c|cosφ gives the height of the parallelipiped. The product of the area of the base and the height gives the volume of the cell.
|a x b| is a scalar, while |a x b|n is a vector that points straight up, and that whose magnitude is the area of the base. If you dot this vector (|a x b|n) with c, you get the volume. One definition for the dot product of a and b is ##a \cdot b = |a| |b| cos(\theta)##, where ##\theta## is the angle between the two vectors. In your problem, the angle is ##\phi##.mysci said:Thanks.
Yes, but why not |axb|, is |axb|(unit vector n) in third step?
mysci said:absinΘ and |axbl are also magnitudes, but |axb|(unit vector n) is a vector. absinΘ = |axb| ≠ |axb|(unit vector n) = vector a x vector b.
However, here absinΘ = |axb|(unit vector n). I don't understand this.
On the other hand, ccosφ is the height of parallelogram, how to change it to vector c? I don't understand it as well.
Thanks.
Mark44 said:|a x b| is a scalar, while |a x b|n is a vector that points straight up, and that whose magnitude is the area of the base. If you dot this vector (|a x b|n) with c, you get the volume. One definition for the dot product of a and b is ##a \cdot b = |a| |b| cos(\theta)##, where ##\theta## is the angle between the two vectors. In your problem, the angle is ##\phi##.
Thanks.Mark44 said:I use LaTeX. Put either two # symbols at the front and two more at the end (for inline) or two $ symbols front and back (for standalone).
Here I'm adding an extra space between each pair so you can see what it looks like without being rendered: # #\vec{a}# #
Removing the spaces gives ##\vec{a}##
Should be |a||b|sinθ = |a x b|. a and b are vectors, so ab is not defined. Both sides of the equation should be scalars, which is why you have the magnitudes (absolute values).mysci said:Thanks.
Then
I got following,
absinΘ = |axb|
The right side is a scalar because it's a dot product, so the left side needs to be a scalar as well.mysci said:ccosΦ = n·c
mysci said:Is it right?
Thank you.Mark44 said:Should be |a||b|sinθ = |a x b|. a and b are vectors, so ab is not defined. Both sides of the equation should be scalars, which is why you have the magnitudes (absolute values).
The right side is a scalar because it's a dot product, so the left side needs to be a scalar as well.
The left side should be |c|cosΦ.
The purpose of studying calculus of crystal structures is to understand the mathematical principles and relationships that govern the atomic and molecular arrangement in a crystal. This knowledge is essential for predicting and manipulating the properties of materials, such as strength, conductivity, and optical properties.
The basic concepts of calculus in crystal structures include mathematical operations like differentiation and integration, vector calculus, and tensor calculus. These concepts are used to describe the geometry and symmetry of crystals, as well as the behavior of atoms and molecules within them.
Calculus is applied in crystallography to analyze diffraction patterns and determine the atomic structure of crystals. It is also used to calculate physical properties of crystals, such as their elastic constants and thermal conductivity.
One of the main challenges of using calculus in crystal structures is the complex and irregular nature of crystal surfaces and defects. This can make it difficult to accurately model and predict the behavior of crystals using calculus-based equations.
Calculus of crystal structures is closely related to other fields of science, such as materials science, physics, and chemistry. It provides a mathematical foundation for understanding the structure and properties of materials, which is essential for advancements in technology and scientific research.