Proof limit derivatave of sin(x)

[Stephanus]

Dear PF Forum,
Continuing our debate discussion in differential in slice of X.
I read this particulare website. About proofing the derivative of sine(x).
http://tutorial.math.lamar.edu/Classes/CalcI/ProofTrigDeriv.aspx

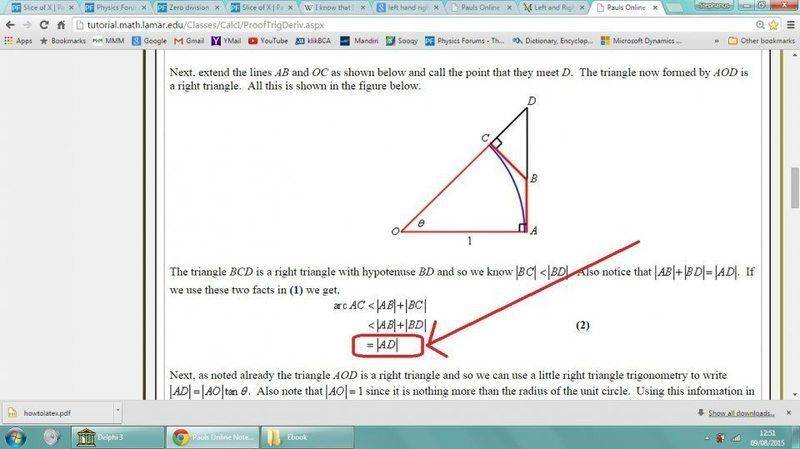
In there, the web writes

arc AC < |AB| + |BC|

       < |AB| + |BD|
       = |AD|

I don't know what the "equal sign" means.
Is this?
A:

arc AC < |AB| + |BC|
arc AC < |AB| + |BD|
arc AC = |AD|

or this?
B:

arc AC < |AB| + |BC|
arc AC < |AB| + |BD|, where |AB| + |BD| = |AD|

 

[Mirero]

Your first interpretation is correct. Get used to that kind of terse writing, it's pretty common.

 

[Stephanus]

Your first interpretation is correct. Get used to that kind of terse writing, it's pretty common.

Which one?
This?
A:
arc AC < |AB| + |BC|
arc AC < |AB| + |BD|
arc AC = |AD|,
but arc AC can't be |AD|. This is my instinct. I just one to know exactly what it means, because in math, a little misinterpretation can lead to big mistake, more with "proof"

 

[Mirero]

Which one?
This?
A:
arc AC < |AB| + |BC|
arc AC < |AB| + |BD|
arc AC = |AD|

Yep.

Moderator note: The answer above is wrong.

 

[Stephanus]

Ok, I understand now.
I read subsequent paragraphs, it's just the way this website formats its answer.
It is.
arc AC < |AB| + |BC|
arc AC < |AB| + |BD|, where |AB| + |BD| = |AD|

 

[Mirero]

Which one?
This?
A:
arc AC < |AB| + |BC|
arc AC < |AB| + |BD|
arc AC = |AD|,
but arc AC can't be |AD|. This is my instinct. I just one to know exactly what it means, because in math, a little misinterpretation can lead to big mistake, more with "proof"

I remember vaguely learning about this. I think they consider that equality for extremely small values of theta. In this case, the limit as theta goes to 0.

 

[Stephanus]

I remember vaguely learning about this. I think they consider that equality for extremely small values of theta. In this case, the limit as theta goes to 0.

No, Mirero, it's just the proof. But

In this case, the limit as theta goes to 0

is tens paragraphs below. It's just the way the web produces its answer. And yes, as theta goes to zero, then arc sin AC = |AD|. But it's not funny to put your answer in the first paragraph.

 

[Mirero]

Ok, I understand now.
I read subsequent paragraphs, it's just the way this website formats its answer.
It is.
arc AC < |AB| + |BC|
arc AC < |AB| + |BD|, where |AB| + |BD| = |AD|

Sorry, I just looked at the diagram again and your interpretation seems to be right. That kind of writing seems weird to me though, and is certainly not conventional.

 

[Stephanus]

Sorry, I just looked at the diagram again and your interpretation seems to be right. That kind of writing seems weird to me though, and is certainly not conventional.

Weird?
You should see this:

This should be arranged to

##\theta = \text{arc AC}##
##\tan\theta = \frac{\sin \theta}{\cos\theta}##
then
##\text{arc AC} < \tan \theta## or
##\text{arc AC} < \frac{\sin \theta}{\cos \theta}## or
##\theta < \tan \theta## or
##\theta < \frac{\sin \theta}{\cos \theta}##
And the web simply writes
##\theta = \text {arc AC} < \tan \theta = \frac{\sin \theta}{\cos \theta}##

 

[Mirero]

Weird?
You should see this:
View attachment 87073
This should be arranged to

##\theta = \text{arc AC}##
##\tan\theta = \frac{\sin \theta}{\cos\theta}##
then
##\text{arc AC} < \tan \theta## or
##\text{arc AC} < \frac{\sin \theta}{\cos \theta}## or
##\theta < \tan \theta## or
##\theta < \frac{\sin \theta}{\cos \theta}##
And the web simply writes
##\theta = \text {arc AC} < \tan \theta = \frac{\sin \theta}{\cos \theta}##

Actually, I would prefer what was written on the website in that case :P

Seems much more succint in my opinion.

 

[Mark44]

arc AC < |AB| + |BC|

       < |AB| + |BD|
       = |AD|

I don't know what the "equal sign" means.
Is this?
A:

[/FONT][/FONT]
[FONT=PT Sans][FONT=Courier New]arc AC < |AB| + |BC|[/FONT][/FONT]
[FONT=PT Sans][FONT=Courier New]arc AC < |AB| + |BD|[/FONT][/FONT]
[FONT=PT Sans][FONT=Courier New]arc AC = |AD|

or this?
B:

[/FONT][/FONT]
[FONT=PT Sans][FONT=Courier New]arc AC < |AB| + |BC|[/FONT][/FONT]
[FONT=PT Sans][FONT=Courier New]arc AC < |AB| + |BD|, where |AB| + |BD| = |AD|

Your first interpretation is correct. Get used to that kind of terse writing, it's pretty common.

NO! The second version is the correct one, not the first.

Version B says this:
arc AC < |AB| + |BC| < |AB| + |BD| = |AD|

In short, arc AC < |AD|

 

[Mirero]

NO! The second version is the correct one, not the first.

Version B says this:
arc AC < |AB| + |BC| < |AB| + |BD| = |AD|

In short, arc AC < |AD|

Yea, I sort of realized that a little too late. I'm much more used to reading flows of equations of the first form, and I guess I do that automatically now. Guess I should be more careful instead of haphazardly going off on my instincts next time.

 

[Stephanus]

NO! The second version is the correct one, not the first.

Version B says this:
arc AC < |AB| + |BC| < |AB| + |BD| = |AD|

In short, arc AC < |AD|

Yeah, that's just the way the website format its output. You of all people know Mark44 that a little incorrect symbol in math will translate a very different thing. Especially for the one who tries to learn mark. But I've solved this problem, it's just how it formats its output.

 

[Mark44]

arc AC < |AB| + |BC|
       < |AB| + |BD|
       = |AD|

I don't know what the "equal sign" means.
Is this?
A:

arc AC < |AB| + |BC|
arc AC < |AB| + |BD|
arc AC = |AD|

As already discussed, no, this is not the same as what's at the top here. Notice that at the top, "arc AC" appears only once, not three times, as you have it just above.

Mixing inequality symbols with equal signs is very common in math texts. For a chain of expressions like this one --

arc AC < |AB| + |BC|
       < |AB| + |BD|
       = |AD|

-- the < sign on the 2nd line refers back to the right side of the previous line. The = sign on the 3rd line refers to the previous (2nd) line.

 

[MidgetDwarf]

the proof is fairly easy, when you think in terms of geometry. We construct the diagram using a unit circle. Therefore the radius is 1.

We have 3 triangles in the diagram. Think of area 1< area 2< area 3.

I can go further.. However i'll give you a hint. what area formulas do you know? Then it is simple algebraic manipulation. Very trivial. Hint. Area of sector is needed.

Another key part in the proof. I won't give the detail. But it is along the same lines.

x^2> x.

however (1/x)> (1/(x^2))

 

[micromass]

This post will not be helpful for the OP, so I suggest that he skips it. This is mainly intended for MidgetDwarf.

the proof is fairly easy, when you think in terms of geometry. We construct the diagram using a unit circle. Therefore the radius is 1.

We have 3 triangles in the diagram. Think of area 1< area 2< area 3.

I can go further.. However i'll give you a hint. what area formulas do you know? Then it is simple algebraic manipulation. Very trivial. Hint. Area of sector is needed.

Another key part in the proof. I won't give the detail. But it is along the same lines.

x^2> x.

however (1/x)> (1/(x^2))

This proof is one of those proofs which are very misleading. It looks very easy, and which has very simply ideas. But when you start thinking deeper, all hell breaks loose. The main problem I always had with this proof is that it used geometry. The problem with geometry is that it is never fleshed out in calculus or analysis textbooks, so strictly speaking, you shouldn't be using it until you do flesh it out. But what the specific problem is, is that you need to have a theory of "areas". Now areas appear very simple. But it is very tricky to define it. In fact, I conjecture that areas such as the area of a circle appear so simple because we have been told this over and over again in elementary school until it was second nature to us. But there is nothing simple about the area of a circle.

Let's start with the question how we would define the area of a circle (or a more general shape). Well, calculus actually gives a very nice answer: the Riemann integral. Yeah, we can just define the area of (half of) a circle to be ##\int_{-1}^1 \sqrt{1-x^2}dx##. OK, but how do we evaluate this? Ah, easy, we use substitution ##x = \sin(u)##. But for that, don't we first need to know that the derivative of the sine equals the cosine? Hmm, yes, we do. But we can easily prove that! Indeed, most calculus books show that by first showing that ##\lim_{h\rightarrow 0} \frac{\sin(h)}{h} = 1##. And how do we prove that? Well, the proof is in the OP, we just compare the area of a circle with... Hmm, so we enter in a circular argument this way...

So yes, I hope I convinced you this way that the proof of ##\lim_{h\rightarrow 0} \frac{\sin(h)}{h}= 1## is not as straightforward as it appears. Now there are essentially two reactions you can have:
1) Wow, why are you being so pedantic. We all know that areas work the way they do. I don't see any reason to doubt it, you can see it clearly!
2) Hmm, this is really annoying me. I must find out more.
Both reactions are acceptable. I agree that I am being pedantic. But it is only (2) which characterizes the mathematician.

 

[MidgetDwarf]

This post will not be helpful for the OP, so I suggest that he skips it. This is mainly intended for MidgetDwarf.
This proof is one of those proofs which are very misleading. It looks very easy, and which has very simply ideas. But when you start thinking deeper, all hell breaks loose. The main problem I always had with this proof is that it used geometry. The problem with geometry is that it is never fleshed out in calculus or analysis textbooks, so strictly speaking, you shouldn't be using it until you do flesh it out. But what the specific problem is, is that you need to have a theory of "areas". Now areas appear very simple. But it is very tricky to define it. In fact, I conjecture that areas such as the area of a circle appear so simple because we have been told this over and over again in elementary school until it was second nature to us. But there is nothing simple about the area of a circle.

Let's start with the question how we would define the area of a circle (or a more general shape). Well, calculus actually gives a very nice answer: the Riemann integral. Yeah, we can just define the area of (half of) a circle to be ##\int_{-1}^1 \sqrt{1-x^2}dx##. OK, but how do we evaluate this? Ah, easy, we use substitution ##x = \sin(u)##. But for that, don't we first need to know that the derivative of the sine equals the cosine? Hmm, yes, we do. But we can easily prove that! Indeed, most calculus books show that by first showing that ##\lim_{h\rightarrow 0} \frac{\sin(h)}{h} = 1##. And how do we prove that? Well, the proof is in the OP, we just compare the area of a circle with... Hmm, so we enter in a circular argument this way...

So yes, I hope I convinced you this way that the proof of ##\lim_{h\rightarrow 0} \frac{\sin(h)}{h}= 1## is not as straightforward as it appears. Now there are essentially two reactions you can have:
1) Wow, why are you being so pedantic. We all know that areas work the way they do. I don't see any reason to doubt it, you can see it clearly!
2) Hmm, this is really annoying me. I must find out more.
Both reactions are acceptable. I agree that I am being pedantic. But it is only (2) which characterizes the mathematician.

Hmm, very insightful post. To me it seemed straight forward because I can "feel" the geometry so to speak. Yes, I can understand your point of how geometry is not put in rigorous footing in these classes.

So, what would be an adequate proof of lim sinx/x? Can you inbox me. I feel it will derail the intention of this thread.

 

[micromass]

Hmm, very insightful post. To me it seemed straight forward because I can "feel" the geometry so to speak.

Well, it is straightforward, except for one little thing: determining the area of a circle. This is highly nontrivial! I will PM you to talk about this further. Anybody else who wishes to discuss this, feel free to PM me or to make a new thread.

 

[disregardthat]

Why is arc AC < |AB| + |BC|? It appears to be taken on face value. How do you prove it? Certainly not by naively calculating the length of the arc and comparing, as this would require knowing the derivatives of the trigonometric functions, which are derived from the fact that ## \lim_{x \to 0} \frac{\sin(x)}{x} = 0##. This goes to show how this proof is actually not that rigorous, it requires a solid definition of arc length, or more generally continuous curve length. There is quite a bit of additional work that will go into proving this inequality.

 

[Stephanus]

This post will not be helpful for the OP, so I suggest that he skips [..]

Ah, I'm too busy, I just read your post. Perhaps it is not useful, but I'll read it anyway. See if there's something that I can learn from this.

 

[Stephanus]

the proof is fairly easy, when you think in terms of geometry. We construct the diagram using a unit circle. Therefore the radius is 1.

We have 3 triangles in the diagram. Think of area 1< area 2< area 3.

I can go further.. However i'll give you a hint. what area formulas do you know? Then it is simple algebraic manipulation. Very trivial. Hint. Area of sector is needed.

Another key part in the proof. I won't give the detail. But it is along the same lines.

x^2> x.

however (1/x)> (1/(x^2))

Hmmm, it's not the proof that I'm asking. It's just how the web format it's output. But through lengthy equation the proof is
##\cos \theta < \frac{\sin \theta}{\theta} < 1##.
So, using layman term. if we 'boost' theta to zero, it will be
##\cos zero < \frac{\sin \theta}{\theta} < 1##, cos zero as we all know is 1.
##1 < \frac{\sin \theta}{\theta} < 1##, so, in tecnical language. ##\frac{\sin \theta}{\theta } = 1!## (btw the exclamation mark is not factorial it's just exclamation mark! )

But that's not the proof that I ask.
It's:
why the website write its format like this.
arc AC < |AB| + |BC|
< |AB| + |BD|
= |AD|,
It's the equal sign that I want to know. But I already know the answer, when I read subsequence paragraphs. It's just how the web format its output.

 

[Mark44]

Hmmm, it's not the proof that I'm asking. It's just how the web format it's output. But through lengthy equation the proof is
##\cos \theta < \frac{\sin \theta}{\theta} < 1##.
So, using layman term. if we 'boost' theta to zero, it will be
##\cos zero < \frac{\sin \theta}{\theta} < 1##, cos zero as we all know is 1.
##1 < \frac{\sin \theta}{\theta} < 1##, so, in tecnical language. ##\frac{\sin \theta}{\theta } = 1!## (btw the exclamation mark is not factorial it's just exclamation mark! )

NO! ##\frac{\sin \theta}{\theta } \neq 1##
But ##\lim_{\theta \to 0} \frac{\sin \theta}{\theta } = 1##
We don't "boost" ##\theta## to zero; we take the limit of each term as ##\theta## approaches zero.

But that's not the proof that I ask.
It's:
why the website write its format like this.
arc AC < |AB| + |BC|
< |AB| + |BD|
= |AD|,
It's the equal sign that I want to know. But I already know the answer, when I read subsequence paragraphs. It's just how the web format its output.

I thought I had answered this question earlier, but apparently you didn't get what I said. It is common in mathematics and physics textbooks to connect multiple expressions using inequality symbols and equal signs. The above is exactly the same as writing this:
arc AC < |AB| + |BC| < |AB| + |BD| = |AD|.

One could write this as a sequence of inequalities and equations, like so:
arc AC < |AB| + |BC|
|AB| + |BC| < |AB| + |BD|
|AB| + |BD| = |AD|

Writing these inequaliies/equations like this takes up more room, and makes it harder to see the main point: that arc AC < |AD|.

In a compound expression using inequalities and equals, the same type of inequality has to be used throughout -- you can't mix in < signs with > signs.

 

[Stephanus]

NO! ##\frac{\sin \theta}{\theta } \neq 1##
But ##\lim_{\theta \to 0} \frac{\sin \theta}{\theta } = 1##
We don't "boost" ##\theta## to zero; we take the limit of each term as ##\theta## approaches zero.

I thought I had answered this question earlier, but apparently you didn't get what I said. It is common in mathematics and physics textbooks to connect multiple expressions using inequality symbols and equal signs. The above is exactly the same as writing this:
arc AC < |AB| + |BC| < |AB| + |BD| = |AD|.

One could write this as a sequence of inequalities and equations, like so:
arc AC < |AB| + |BC|
|AB| + |BC| < |AB| + |BD|
|AB| + |BD| = |AD|

Writing these inequaliies/equations like this takes up more room, and makes it harder to see the main point: that arc AC < |AD|.

In a compound expression using inequalities and equals, the same type of inequality has to be used throughout -- you can't mix in < signs with > signs.

Come on, Mark44.
I have already had the answers days ago, but for several post, members weren't answering my question. They discuss the proof of sine x.
Which is not what I asked. I just asked why the format is
arc AC < |AB| + |BC|
< |AB| + |BD|
= |AD|
And for this I have already had the answer days before. Perhaps my title is misleading.
The answer is, as you wrote,

arc AC < |AB| + |BC|
|AB| + |BC| < |AB| + |BD|
|AB| + |BD| = |AD|

The web should write like that to avoid misunderstanding.

And for proof of sine x...?
Well, I have learned the proof also.
See this equation.
##\cos \theta \lt \frac{\sin \theta}{\theta} \lt 1##
or I could write
##\cos \theta \lt X \lt 1##
Than, if we boost theta to zero, than ##\cos \theta## must be 1. So
##1 \lt X \lt 1##, even if this is not the correct mathematic formula. Technically, X is squeezed between 1 and 1, so I'm convinced that X is none other than 1.
So ##\frac{\sin \theta}{\theta} = 1## if theta is almost zero.
But we all had this concept in high school, right. Just forgot the proof. Now I see the proof clearly.

 

[micromass]

##\cos \theta \lt X \lt 1##
Than, if we boost theta to zero, than ##\cos \theta## must be 1. So

Again, you don't boost theta to zero. This is an incorrect way of seeing things.
You might think you have the right ideas and concepts, but you don't. There are some major flaws in your mathematics, and that will come back later to haunt you. It is crucial to learn the correct notation and the correct way of doing things. And I'm afraid that just reading some online websites are not teaching you this.

 

[Mark44]

Come on, Mark44.
I have already had the answers days ago, but for several post, members weren't answering my question. They discuss the proof of sine x.
Which is not what I asked. I just asked why the format is
arc AC < |AB| + |BC|
< |AB| + |BD|
= |AD|
And for this I have already had the answer days before. Perhaps my title is misleading.
The answer is, as you wrote,

arc AC < |AB| + |BC|
|AB| + |BC| < |AB| + |BD|
|AB| + |BD| = |AD|

The web should write like that to avoid misunderstanding.

Or, since the shorter way of writing is so commonly used, you could learn to understand it.

As already mentioned, the longer form takes up more space for not much gain in clarity.

And for proof of sine x...?
Well, I have learned the proof also.
See this equation.
##\cos \theta \lt \frac{\sin \theta}{\theta} \lt 1##
or I could write
##\cos \theta \lt X \lt 1##
Than, if we boost theta to zero, than ##\cos \theta## must be 1. So
##1 \lt X \lt 1##, even if this is not the correct mathematic formula. Technically, X is squeezed between 1 and 1, so I'm convinced that X is none other than 1.
So ##\frac{\sin \theta}{\theta} = 1## if theta is almost zero.

How big is "almost zero"? Is .00001 almost zero? If so, ##\frac{\sin \theta}{\theta}## still isn't equal to zero.

As long as ##\theta## is different from zero, ##\frac{\sin \theta}{\theta}## will be different from 1. What we can say, though, is ##\lim_{\theta \to 0}\frac{\sin \theta}{\theta} = 1##. IOW, the limit of this fraction is 1, even though ##\frac{\sin \theta}{\theta}## is never equal to 1 for any nonzero value of ##\theta##.

But we all had this concept in high school, right. Just forgot the proof. Now I see the proof clearly.

 

[Stephanus]

Again, you don't boost theta to zero. This is an incorrect way of seeing things.
You might think you have the right ideas and concepts, but you don't. There are some major flaws in your mathematics, and that will come back later to haunt you. It is crucial to learn the correct notation and the correct way of doing things. And I'm afraid that just reading some online websites are not teaching you this.

"Boost", yes. I choose the 'non mathematic' word. I say that we should solve this problem technically not mathematically.
Okay...

For those who can answer my question (especially you Micromass ) don't need this picture. But I show it anyway, so we are at the same prespective.
So through a lengthy calculations we come up at this
##\cos \theta \lt \frac{\sin \theta}{\theta} \lt 1##
Now theta could be as low as 0 and as high as 1/2 pi.
when theta is 1/2 pi there are range of possibility for ##\frac{\sin \theta}{\theta}##. It's in the range between 0 and 1. Altough we all know the answer for ##\theta = \frac{1}{2} \pi## is ##\frac{\sin \frac{1}{2}\pi}{\frac{1}{2} \pi} = \frac{2}{\pi} ##
theta = 1/3 pi, the range for ##\frac{\sin \theta}{\theta}## at quick glance is between ##0.5 \text{ to } 1##. Answer: ##\frac{3\sqrt{3}}{2\pi}##
theta = 1/4 pi, range is ##\frac{1}{2}\sqrt{2} \text{ to } 1##. Answer: ##\frac{2\sqrt{2}}{\pi}##
theta ≈ 0, range is ##≈1 \to 1##, so deducting by this logic. ##\frac{\sin \theta}{\theta}## is 1 if theta is almost zero.
Is this the wrong way to think?

 

[Mark44]

"Boost", yes. I choose the 'non mathematic' word. I say that we should solve this problem technically not mathematically.
Okay...
View attachment 87189
For those who can answer my question (especially you Micromass ) don't need this picture. But I show it anyway, so we are at the same prespective.
So through a lengthy calculations we come up at this
##\cos \theta \lt \frac{\sin \theta}{\theta} \lt 1##
Now theta could be as low as 0 and as high as 1/2 pi.
when theta is 1/2 pi there are range of possibility for ##\frac{\sin \theta}{\theta}##. It's in the range between 0 and 1. Altough we all know the answer for ##\theta = \frac{1}{2} \pi## is ##\frac{\sin \frac{1}{2}\pi}{\frac{1}{2} \pi} = \frac{2}{\pi} ##
theta = 1/3 pi, the range for ##\frac{\sin \theta}{\theta}## at quick glance is between ##0.5 \text{ to } 1##. Answer: ##\frac{3\sqrt{3}}{2\pi}##
theta = 1/4 pi, range is ##\frac{1}{2}\sqrt{2} \text{ to } 1##. Answer: ##\frac{2\sqrt{2}}{\pi}##
theta ≈ 0, range is ##≈1 \to 1##, so deducting by this logic. ##\frac{\sin \theta}{\theta}## is 1 if theta is almost zero.
Is this the wrong way to think?

Yes, it's the wrong way to think.
##\frac{\sin \theta}{\theta}## is undefined if ##\theta## = 0, and if ##\theta## is near zero, ##\frac{\sin \theta}{\theta}## will be only near 1, but won't be equal to 1. So it's incorrect to say "##\frac{\sin \theta}{\theta}## = 1" or "##\frac{\sin \theta}{\theta}## is 1" if ##\theta## is "almost zero." No matter how close ##\theta## is to 0, ##\frac{\sin \theta}{\theta} \neq 1##.

That's where the concept of the limit comes in. It is correct to say ##\lim_{\theta \to 0} \frac{\sin \theta}{\theta} = 1##, with an emphasis on the limit part.

 

[Stephanus]

Yes, it's the wrong way to think.

Thanks

##\frac{\sin \theta}{\theta}## is undefined if ##\theta## = 0

Ok

, and if ##\theta## is near zero, ##\frac{\sin \theta}{\theta}## will be only near 1, but won't be equal to 1.

Ok

So it's incorrect to say "##\frac{\sin \theta}{\theta}## = 1" or "##\frac{\sin \theta}{\theta}## is 1" if ##\theta## is "almost zero."

Ok

No matter how close ##\theta## is to 0, ##\frac{\sin \theta}{\theta} \neq 1##.

Ok

That's where the concept of the limit comes in. It is correct to say ##\lim_{\theta \to 0} \frac{\sin \theta}{\theta} = 1##, with an emphasis on the limit part.

Okay. I'm satisfied with your answer. For an amateur like me, confirmation is the nicest thing than guess it by myself. Can't trust myself you know. I have ideas, but I don't know if my ideas are right or wrong. Your approval (or disapproval) is important for me.

 

[Stephanus]

Okay..., now let me ask for confirmation.
##\lim_{h \to 0}##

A: ##\sin(h)##
- Is there a limit in there? The left hand/right hand limit is not equal, but very very close, right.?
- If there is a limit, what is its value? 0?

B: ##\cos(h)##
- Is there a limit in there? The left/right hand limit is equal, right?
- What is its value? 1?

What is the derivative of Sin (x)?
##\frac{\sin(x+h) - \sin(x)}{(x+h)-x}##

##\frac{\sin(x)\cos(h) + \sin(h)\cos(x) - \sin(x)}{h}##

##\frac{\sin(x)\cos(h) - \sin(x) + \sin(h)\cos(x)}{h}##C: ##\frac{\sin (x)(\cos(h) - 1)}{h} = \sin (x) \frac{\cos(h)-1}{h}##
- Is there a limit there? Is the left/right hand limit equal?
- What is its value? Sin(x)? 0?

D: ##\frac{\cos(h) - 1}{h}##
- Is there a limit there? Is the left/right hand limit equal?
- What is its value? 1 ? 0?

 

[pbuk]

A: ##\sin(h)##
- Is there a limit in there? The left hand/right hand limit is not equal, but very very close, right.?
- If there is a limit, what is its value? 0?

sin(0) = 0 so we do not need to consider limits.

B: ##\cos(h)##
- Is there a limit in there? The left/right hand limit is equal, right?
- What is its value? 1?

cos(0) = 1 so we do not need to consider limits.

What is the derivative of Sin (x)? ## \frac{\sin(x+h) - \sin(x)}{(x+h)-x} ##

Yes, but because ## (x + h) - x = (h + x) - x = h + (x - x) = h ## we would write $$ \frac{d(\sin x)}{dx} = \lim_{h \to 0} \frac{\sin(x+h) - \sin(x)}{h} $$

##\frac{\sin(x)\cos(h) + \sin(h)\cos(x) - \sin(x)}{h}##

Yes, by the trigonometric identity ## \sin(a + b) = \sin a \cos b + \cos a \sin b ## this can be seen to be equal to the previous expression.

##\frac{\sin(x)\cos(h) - \sin(x) + \sin(h)\cos(x)}{h}##

This expression is identical to the previous one due to the commutativity of addition and subtraction.

D: ##\frac{\cos(h) - 1}{h}##
- Is there a limit there? Is the left/right hand limit equal?
- What is its value? 1 ? 0?

(I changed the order of your questions, you'll see why in a minute). To find this limit we can use the expansion ## \cos h = 1 - \frac{h^2}{2!} + \frac{h^4}{4!} ... ##. We then have
$$ \lim_{h \to 0} \frac{\cos(h)-1}{h}
= \lim_{h \to 0} \frac{(1 - \frac{h^2}{2!} + \frac{h^4}{4!} ...)-1}{h}
= \lim_{h \to 0} \frac{-\frac{h^2}{2!} + \frac{h^4}{4!} ...}{h}
= \lim_{h \to 0} \bigg(-\frac{h}{2!} + \frac{h^3}{4!} ... \bigg)
= 0 $$
Because the limit exists the left hand limit and right hand limit are equal.

C: ##\frac{\sin (x)(\cos(h) - 1)}{h} = \sin (x) \frac{\cos(h)-1}{h}##
- Is there a limit there? Is the left/right hand limit equal?
- What is its value? Sin(x)? 0?

Using the result from D we have
$$ \lim_{h \to 0} \bigg( \sin (x) \frac{\cos(h)-1}{h} \bigg) = \sin (x) \lim_{h \to 0} \frac{\cos(h)-1}{h} = \sin (x) \cdot 0 = 0 $$
Because the limit exists the left hand limit and right hand limit are equal.

 

[Stephanus]

sin(0) = 0 so we do not need to consider limits.

I mean ##\lim_{h \to 0} \sin(h)##

Is there a limit in ##\lim_{h \to 0} \sin(h)##?
What is the result? 0 or ≈ 0?
Left/Right hand is not equal, right?

cos(0) = 1 so we do not need to consider limits.

I mean ##\lim_{h \to 0} \cos(h)##

Is there a limit in ##\lim_{h \to 0} \cos(h)##?
Left/Right hand is equal, right.
The result? 1 or ≈ 1?

sin(0) = 0 so we do not need to consider limits.

Yes, but because ## (x + h) - x = (h + x) - x = h + (x - x) = h ## we would write $$ \frac{d(\sin x)}{dx} = \lim_{h \to 0} \frac{\sin(x+h) - \sin(x)}{h} $$[..][/QUOTE]Still reading the rest...

 

[micromass]

Is there a limit in ##\lim_{h \to 0} \sin(h)##?
What is the result? 0 or ≈ 0?

It is =0.

Left/Right hand is not equal, right?

They are equal.

Is there a limit in ##\lim_{h \to 0} \cos(h)##?

=1

Left/Right hand is equal, right.

Yes.

 

[pbuk]

I mean ##\lim_{h \to 0} \sin(h)##

I know you do. Because sin(h) is continuous, in particular it is continuous at h = 0 (which implies that it is defined at h = 0), by definition ## \lim_{h \to 0} \sin(h) = \sin(0) = 0 ##, so we don't need to do any working out we simply write sin(0) = 0. Likewise by definition ## \lim_{h \to 0} \cos(0) = \cos(0) = 1 ##.
We can't do this with ## \lim_{x \to 0} \frac{\sin x}{x} ## because ## \frac{\sin x}{x} ## is not defined at x = 0.

(Edited to improve accuracy of statements regarding definition/continuity)

 

[Stephanus]

I know you do. Because sin(h) is continuous, in particular it is continuous at h = 0, by definition ## \lim_{h \to 0} \sin(h) = \sin(0) = 0 ##, so we don't need to do any working out we simply write sin(0) = 0. Likewise by definition ## \lim_{h \to 0} \cos(0) = \cos(0) = 1 ##.
We can't do this with ## \lim_{x \to 0} \frac{\sin x}{x} ## because ## \frac{\sin x}{x} ## has a discontinuity at x = 0.

So, "continuous", "left hand", "right hand". Ok, I'll study them.
Btw, tangent/cotangent are not continuous, right?

 

[micromass]

So, "continuous", "left hand", "right hand". Ok, I'll study them.
Btw, tangent/cotangent are not continuous, right?

They are continuous wherever they are defined.