Paraxial approximation on concave mirror

[zicron]

1. Find the length of the curvature of a concave mirror of 20cm that comply with paraxial approximation for all incident rays


2.conventional geometry formula , sinθ≈θ or tanθ≈θ for paraxial rays


3. I had try drafting out the diagram , labeling all the unknown angle with symbol and trying to work out on them but I just can't find the angle CAB of the triangle because I don't know height of the triangle.

This is a sketch:

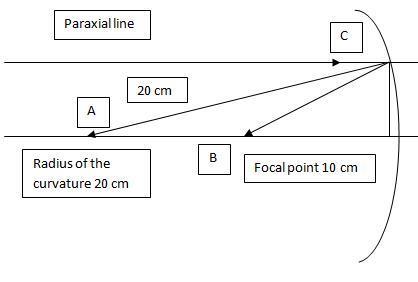
Did I miss anything?
Any suggestion on how to solve this problem?

 

[Redbelly98]

I'm pretty familiar with basic optics, but have trouble understanding this question.
What is meant by "length of the curvature"?
Also, what is the condition for complying with the paraxial approximation?

 

[zicron]

The incoming rays is parallel to the ray axis.
According to the definition from the book : Rays that make small angle (such that sinθ≈θ ) with the mirror's axis are called paraxial rays.In the paraxial approximation only the paraxial rays are considered.
The length of the curvature is the curve where reflected ray is comply with the paraxial approximation (the curve next to the height of the triangle I draw).The main problem is I don't know how to find the angle of CAB to ascertain the length of the curvature.

 

[Redbelly98]

The incoming rays is parallel to the ray axis.
According to the definition from the book : Rays that make small angle (such that sinθ≈θ ) with the mirror's axis are called paraxial rays.In the paraxial approximation only the paraxial rays are considered.

Okay, but you (or somebody) has to decide: what is the maximum angle for which sinθ≈θ is true? Is it when sinθ and θ differ by 1%? Or 10%? Or something else? Does your professor or textbook provide the criterion? If not, the problem cannot be solved.

The length of the curvature is the curve where reflected ray is comply with the paraxial approximation (the curve next to the height of the triangle I draw).The main problem is I don't know how to find the angle of CAB to ascertain the length of the curvature.

Thanks for clarifying.
The angle of the reflected ray is CAO, where O is at the center of the lens.
As an approximation, you could assume the ray passes through the focal point. You'll have to use some trigonometry to figure out the angle.

 

[zicron]

Well,there are only 2 things I know about this triangle which is AB = 10 cm and AC = 20 cm , all the rest are remain unknown.I try to solve it using trigonometry method such as A/sinA=B/sinB=C/sinC and theorem pythagoras but still I am stuck in this question.

l is the length of the whole triangle, h is the height of the triangle and [tex]\theta[/tex] is the angle of CAO.

[tex]\frac{20}{sin90}[/tex]=[tex]\frac{l}{sin(90-\theta)}[/tex]=[tex]\frac{h}{sin\theta}[/tex]
since sin(90-[tex]\theta[/tex])= cos[tex]\theta[/tex]
after rearranging the formula
l=20cos[tex]\theta[/tex] and h=20sin[tex]\theta[/tex]

CB²=h²+(l-10)²

I am stuck here and don't know how to relate them in this step,any clue?

 

[Redbelly98]

My apologies. The reflected ray is CB, not CA. And angle CBO is the reflected angle θ (not CAO as I said earlier). So let angle CBO be θ_max, the largest angle for which sinθ≈θ is an acceptable approximation.

You can proceed as you were doing, solving triangle ABC to get the length of side BC. You know the lengths of sides AB and AC, and also that angle ABC=180-θ_max

Once you have the length of BC, you can use sinθ_max to find h.

 

[zicron]

CB²=h²+(l-10)²

=h²+l²-20l+100
=(h²+l²)-20l+100
since sin²θ+cos²θ=1
=20²-20l+100
=500-20l

For triangle ABC , there is another unknown angle(ACB) and I will label as [tex]\theta[/tex]_ACB

[tex]\frac{20}{sin(180-\theta)}[/tex]=[tex]\frac{CB}{sin\theta}[/tex]=[tex]\frac{10}{sin\theta_{ACB}}[/tex]

so by substituting CB = 500-20l

[tex]\frac{20}{500-20l}[/tex]=[tex]\frac{sin(180-\theta)}{sin\theta}[/tex]

so am I doing it right?

 

[Redbelly98]

CB²=h²+(l-10)²

=h²+l²-20l+100
=(h²+l²)-20l+100
since sin²θ+cos²θ=1
=20²-20l+100
=500-20l

While this is correct, I think sinθ=h/CB is probably more useful.

For triangle ABC , there is another unknown angle(ACB) and I will label as [tex]\theta[/tex]_ACB

[tex]\frac{20}{sin(180-\theta)}[/tex]=[tex]\frac{CB}{sin\theta}[/tex]=[tex]\frac{10}{sin\theta_{ACB}}[/tex]

Problem: on the left-hand term, you are using θ for <CBO. But in the middle term, you are saying θ is <CAB.
I was using θ = <CBO, as that it is the angle-from-horizontal for the reflected ray CB. I.e., it is the angle for which the condition sinθ≈θ is to be applied.

so by substituting CB = 500-20l

No, CB² = 500 - 20l.
Instead, I recommend using the law of cosines here, using the angle <ABC which is 180-θ.