- #1
Math Amateur
Gold Member
MHB
- 3,998
- 48
I am reading Hugo D. Junghenn's book: "A Course in Real Analysis" ...
I am currently focused on Chapter 9: "Differentiation on ##\mathbb{R}^n##"
I need some help with the proof of Proposition 9.2.3 ...
Proposition 9.2.3 and the preceding relevant Definition 9.2.2 read as follows:

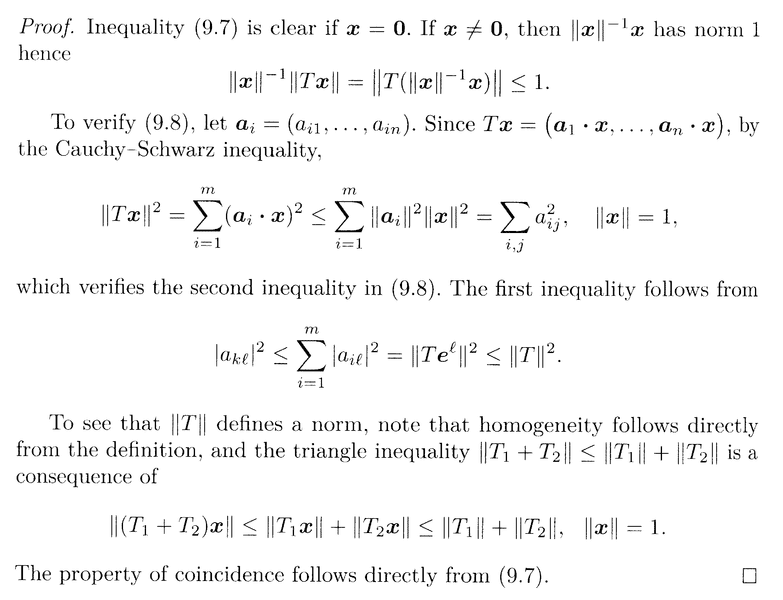
In the above proof Junghenn let's ##\mathbf{a}_i = ( a_{i1}, a_{i2}, \ ... \ ... \ , a_{in} ) ##
and then states that##T \mathbf{x} = ( \mathbf{a}_1 \cdot \mathbf{x}, \mathbf{a}_2 \cdot \mathbf{x}, \ ... \ ... \ , \mathbf{a}_n \cdot \mathbf{x} ) ## where ##\mathbf{x} = ( x_1, x_2, \ ... \ ... \ x_n )##(Note: Junghenn defines vectors in ##\mathbb{R}^n## as row vectors ... ... )Now I believe I can show ##T \mathbf{x}^t = [a_{ij} ]_{ m \times n } \mathbf{x}^t = ( \mathbf{a}_1 \cdot \mathbf{x}, \mathbf{a}_2 \cdot \mathbf{x}, \ ... \ ... \ , \mathbf{a}_n \cdot \mathbf{x} )^t ## ...
... ... as follows:##T \mathbf{x}^t = [a_{ij} ]_{ m \times n } \mathbf{x}^t = \begin{pmatrix} a_{11} & a_{12} & ... & ... & a_{1n} \\ a_{21} & a_{22} & ... & ... & a_{2n} \\ ... & ... & ... & ... & ... \\ ... & ... & ... & ... & ... \\ a_{m1} & a_{m2} & ... & ... & a_{mn} \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ . \\ . \\ x_n \end{pmatrix}####= \begin{pmatrix} a_{11} x_1 + a_{12} x_2 + \ ... \ ... \ + a_{1n} x_n \\ a_{21} x_1 + a_{22} x_2 + \ ... \ ... \ + a_{2n} x_n \\ ... \\ ... \\ a_{m1} x_1 + a_{m2} x_2 + \ ... \ ... \ + a_{mn} x_n \end{pmatrix}####= \begin{pmatrix} \mathbf{a}_1 \cdot \mathbf{x} \\ \mathbf{a}_2 \cdot \mathbf{x} \\ . \\ . \\ \mathbf{a}_n \cdot \mathbf{x} \end{pmatrix}##
##= ( \mathbf{a}_1 \cdot \mathbf{x}, \mathbf{a}_2 \cdot \mathbf{x}, \ ... \ ... \ , \mathbf{a}_n \cdot \mathbf{x} )^t ##
So ... I have shown##T \mathbf{x}^t = [a_{ij} ]_{ m \times n } \mathbf{x}^t = ( \mathbf{a}_1 \cdot \mathbf{x}, \mathbf{a}_2 \cdot \mathbf{x}, \ ... \ ... \ , \mathbf{a}_n \cdot \mathbf{x} )^t##...How do I reconcile or 'square' that with Junghenn's statement that##T \mathbf{x} = ( \mathbf{a}_1 \cdot \mathbf{x}, \mathbf{a}_2 \cdot \mathbf{x}, \ ... \ ... \ , \mathbf{a}_n \cdot \mathbf{x} )## where ##\mathbf{x} = ( x_1, x_2, \ ... \ ... \ x_n )##(Note: I don't think that taking the transpose of both sides works ... ?)
Hope someone can help ...
Peter
I am currently focused on Chapter 9: "Differentiation on ##\mathbb{R}^n##"
I need some help with the proof of Proposition 9.2.3 ...
Proposition 9.2.3 and the preceding relevant Definition 9.2.2 read as follows:
In the above proof Junghenn let's ##\mathbf{a}_i = ( a_{i1}, a_{i2}, \ ... \ ... \ , a_{in} ) ##
and then states that##T \mathbf{x} = ( \mathbf{a}_1 \cdot \mathbf{x}, \mathbf{a}_2 \cdot \mathbf{x}, \ ... \ ... \ , \mathbf{a}_n \cdot \mathbf{x} ) ## where ##\mathbf{x} = ( x_1, x_2, \ ... \ ... \ x_n )##(Note: Junghenn defines vectors in ##\mathbb{R}^n## as row vectors ... ... )Now I believe I can show ##T \mathbf{x}^t = [a_{ij} ]_{ m \times n } \mathbf{x}^t = ( \mathbf{a}_1 \cdot \mathbf{x}, \mathbf{a}_2 \cdot \mathbf{x}, \ ... \ ... \ , \mathbf{a}_n \cdot \mathbf{x} )^t ## ...
... ... as follows:##T \mathbf{x}^t = [a_{ij} ]_{ m \times n } \mathbf{x}^t = \begin{pmatrix} a_{11} & a_{12} & ... & ... & a_{1n} \\ a_{21} & a_{22} & ... & ... & a_{2n} \\ ... & ... & ... & ... & ... \\ ... & ... & ... & ... & ... \\ a_{m1} & a_{m2} & ... & ... & a_{mn} \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ . \\ . \\ x_n \end{pmatrix}####= \begin{pmatrix} a_{11} x_1 + a_{12} x_2 + \ ... \ ... \ + a_{1n} x_n \\ a_{21} x_1 + a_{22} x_2 + \ ... \ ... \ + a_{2n} x_n \\ ... \\ ... \\ a_{m1} x_1 + a_{m2} x_2 + \ ... \ ... \ + a_{mn} x_n \end{pmatrix}####= \begin{pmatrix} \mathbf{a}_1 \cdot \mathbf{x} \\ \mathbf{a}_2 \cdot \mathbf{x} \\ . \\ . \\ \mathbf{a}_n \cdot \mathbf{x} \end{pmatrix}##
##= ( \mathbf{a}_1 \cdot \mathbf{x}, \mathbf{a}_2 \cdot \mathbf{x}, \ ... \ ... \ , \mathbf{a}_n \cdot \mathbf{x} )^t ##
So ... I have shown##T \mathbf{x}^t = [a_{ij} ]_{ m \times n } \mathbf{x}^t = ( \mathbf{a}_1 \cdot \mathbf{x}, \mathbf{a}_2 \cdot \mathbf{x}, \ ... \ ... \ , \mathbf{a}_n \cdot \mathbf{x} )^t##...How do I reconcile or 'square' that with Junghenn's statement that##T \mathbf{x} = ( \mathbf{a}_1 \cdot \mathbf{x}, \mathbf{a}_2 \cdot \mathbf{x}, \ ... \ ... \ , \mathbf{a}_n \cdot \mathbf{x} )## where ##\mathbf{x} = ( x_1, x_2, \ ... \ ... \ x_n )##(Note: I don't think that taking the transpose of both sides works ... ?)
Hope someone can help ...
Peter
Attachments
Last edited:



