- #1
Nat3
- 69
- 0
I'm working my way through a solution of a problem and am confused on a step where a differentiation is performed. I'm sure I'm just forgetting some kind of rule, but I've been perusing my textbook and can't seem to figure out what I'm missing. Here's the step I'm talking about:
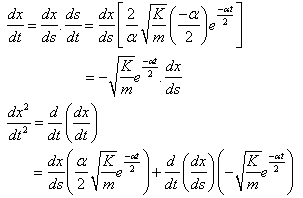
Note that there's a typo in the solution: [itex]\frac{dx^2}{dt^2}[/itex] should be [itex]\frac{d^2x}{dt^2}[/itex].
The top part I understand completely, it's the bottom half I'm confused about. It seems to me that:
[itex]\frac{d^2x}{dt^2} = \frac{d}{dt}(\frac{dx}{dt}) = \frac{dx}{ds}(\frac{\alpha}{2}\sqrt{\frac{K}{m}}e^{-\frac{\alpha t}{2}})[/itex]
In other words, I don't understand where the second group of terms (after the + sign) comes from in the last line. Why is it there?
Note that there's a typo in the solution: [itex]\frac{dx^2}{dt^2}[/itex] should be [itex]\frac{d^2x}{dt^2}[/itex].
The top part I understand completely, it's the bottom half I'm confused about. It seems to me that:
[itex]\frac{d^2x}{dt^2} = \frac{d}{dt}(\frac{dx}{dt}) = \frac{dx}{ds}(\frac{\alpha}{2}\sqrt{\frac{K}{m}}e^{-\frac{\alpha t}{2}})[/itex]
In other words, I don't understand where the second group of terms (after the + sign) comes from in the last line. Why is it there?