Natural position of a string wrapping around a cone

[dawin]

I've had a problem I encountered at work some time ago and took a personal interest in. I never did end up solving it, but I've recently looked at it again.

It goes like this:

You have an axisymmetric part, such as a cone, and it's positioned such that its central axis is coincident and parallel to the central axis of a ring.

A string comes from this ring and attaches to the tip. Viewing the from the side, the string forms an angle with the part's axis, [itex]\theta[/itex], where [itex]90^\circ[/itex] means the string is perpendicular to the central axis. The part then undergoes a rotation, [itex]\phi[/itex], that causes the string to wrap around it. Assuming the string is not slipping, it will naturally "walk up" the part until it reaches [itex]90^\circ[/itex]. (I've attached a schematic)

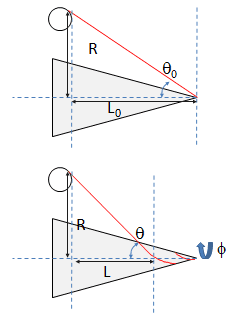
I'd like to determine the function that defines the natural walk-up, but I think I'm getting hung up on some assumptions.

Assume a very small rotation [itex]\phi[/itex] that will produce some walk-up. For a cone, the radius is a function of the axial distance from the initial point, [itex]z[/itex]. If I take the "traversed" area, and unravel the cone, I end up with a flattened frustum (I'm trying to assume a general case); I simplified this to a trapezoid with the string's path mapped between two corners (attachment 2--sorry, I'm drawing these in PowerPoint). Here's one area I think I might be going wrong, but don't see intuitively if this would really affect the angle.

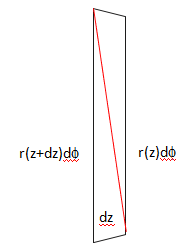
I'm assuming that for a very small rotation, that path will form a straight line (I think this could be where I'm going wrong, but I'm not sure how else to define the path!).

If the large ring's radius is constant, [itex]R[/itex], and the initial distance the string attaches to from this ring is [itex]L[/itex], then the initial angle is:

[itex] \theta_0 = tan^{-1}(R/L_0) [/itex]

If I look at my trapezoid, the arc produced by the rotation is [itex]s_1 = r(z)d\phi[/itex]; the arc where the string ended after rotation is [itex]s_2 = r(z + dz)d\phi[/itex].

This change in position, [itex]dz[/itex] will change the "attachment" length to [itex]L = L_0 - dz[/itex], which changes the angle. I'd naturally want to calculate any new angle as:

[itex]
\theta = tan^{-1}(R/(L-z))
[/itex]

But in my case, I keep ending up with [itex]\theta[/itex] as functions of [itex]L-z[/itex], and feel like I'm sticking myself in a loop. I tried approach it with the chain rule, trying to solve two separate relations [itex]\frac{d\theta}{dz}\frac{dz}{d\phi}=\frac{d\theta}{d\phi}[/itex] but feel like I'm just butchering it here.

If I choose a small enough [itex]\phi[/itex], sure, I can iterate this and get something I believe is close. But I'd like to know how to get to a closed-form solution. There are approaches out there for filament winding, but these account for a different payout eye setup. Plus, they assume the line follows a geodesic to ignore friction, which I don't necessarily need to do in this case (there are ways to keep the fiber in place).

 

[jvicens]

Dear colleague,

Thank you for sharing your interesting problem with us. After studying your forum post and the attached diagrams, I have some suggestions that might help you in finding a solution.

Firstly, I would like to point out that your assumption about the path forming a straight line for a very small rotation may not be entirely accurate. In reality, as the cone rotates, the string will experience some tension and may not follow a perfectly straight path. This tension can be caused by various factors such as the weight of the string, friction, and the shape of the cone. Therefore, it might be more appropriate to consider the string's path as a curve rather than a straight line.

Secondly, I believe your approach using the chain rule is on the right track. However, instead of trying to solve two separate relations, I would suggest considering the arc length of the string as a function of both \phi and z. This can be expressed as:

s = \int_{z}^{z+dz} \sqrt{r^2(z) + \left(\frac{dz}{d\phi}\right)^2} d\phi

where r(z) is the radius of the cone at the axial distance z, and \frac{dz}{d\phi} is the change in axial distance due to the rotation.

Using this expression, we can determine the angle \theta as:

\theta = tan^{-1}\left(\frac{R}{L-z}\right) = tan^{-1}\left(\frac{R}{L_0-s}\right)

where L_0 is the initial distance of the string attachment from the ring, and s is the arc length of the string as defined above.

I hope these suggestions will help you in finding a closed-form solution for your problem. If you have any further questions or would like to discuss this further, please do not hesitate to reach out.

Best of luck in your research!