- #1
NeuralNet
- 24
- 0
I am trying to stabilize an inverted pendulum with a physical system as follows:
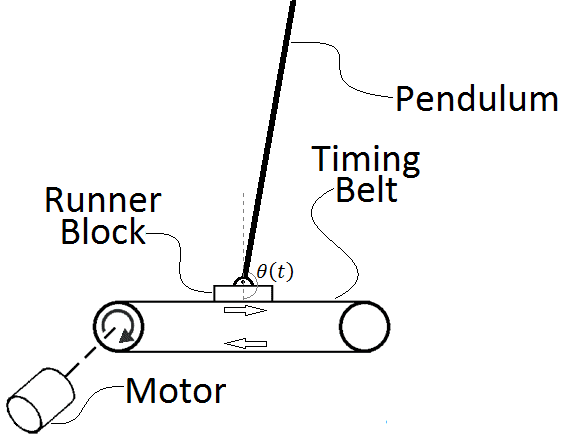
The measured values of the pendlums angle and the cart (runner block) position are sent to a digital controller. The digital controller then outputs a value that is sent to the motor to turn the belt pulley system which in turn moves the cart.
The problem I am having is my equations are such that the value coming out of the controller is the force (in Newtons) that needs to be applied to the cart to move it. I need to convert the force value to the torque value at the motor.
How do I do that?
I am an EE major, and don't know too much about ME stuff. Any help is much appreciated.
The measured values of the pendlums angle and the cart (runner block) position are sent to a digital controller. The digital controller then outputs a value that is sent to the motor to turn the belt pulley system which in turn moves the cart.
The problem I am having is my equations are such that the value coming out of the controller is the force (in Newtons) that needs to be applied to the cart to move it. I need to convert the force value to the torque value at the motor.
How do I do that?
I am an EE major, and don't know too much about ME stuff. Any help is much appreciated.
Last edited: