- #71
- 22,183
- 3,321
Awesome, it appears (a) and (c) are solved then.
TeethWhitener said:Ok, I'll try advanced problem number 7. First, we note that ##X=b\tan{\theta}##. To get the expected value of ##X##, we use the law of the unconcscious statistician:
$$E[X(\theta)] = \int^{\frac{\pi}{2}}_{-\frac{\pi}{2}} X(\theta) f(\theta)d\theta$$
where ##f(\theta)## is the probability density function of ##\theta##. We know that ##\theta## is uniformly distributed over ##(-\pi/2,\pi/2)##, so ##f(\theta) = 1/\pi##. Thus the expected value of ##X## is
$$E[X(\theta)] =\frac{b}{\pi} \int^{\frac{\pi}{2}}_{-\frac{\pi}{2}} \tan{\theta} d\theta$$
Since ##\tan \theta## is an odd function and the integration is symmetric about ##x=0##, the expected value is ##E[X] = 0##.
For the variance, we have:
$$\sigma^2 = E([X^2])-(E[X])^2$$
so we need to evaluate ##E([X^2])##. We use the unconscious statistician again, which gives us the integral:
$$E[X^2] = \frac{b^2}{\pi} \int^{\frac{\pi}{2}}_{-\frac{\pi}{2}} \tan^2{\theta} d\theta$$
This integral diverges to infinity as we take the bounds of integration out to ##\pm \pi/2##. This would imply that the variance is infinite ##(\sigma^2 = \infty)##. I'm not sure if this is right, but my intuition says this makes sense, since there's a finite probability of ##|X|## being arbitrarily large. But I don't know that for certain, and I'm not sure how to make it more mathy.
Did I cut too many corners? Upon closer inspection, I getmicromass said:Your expected value is wrong.
Really? As far as I can see, the symmetry of the problem implies that the expectation is ##0##. If we take two infinitesimal intervals ##[-x-dx, x]## and ##[x,x+dx]## on the wall, corresponding to the angle intervals ##[-\theta-d\theta, \theta]## and ##[\theta,\theta+d\theta]##, respectively, both having probability ##d\theta/\pi##, their contributions to the expectation are ##-xd\theta/\pi## and ##xd\theta/\pi##, respectively, so they cancel each other out. Every infinitesimal interval has such a "mirror" interval on the other side of ##a##, so the expectation must be ##0##.micromass said:Your expected value is wrong.
Then by that same reasoning, would you say that ##\int_{-\infty}^{+\infty} xdx = 0## too?Erland said:Really? As far as I can see, the symmetry of the problem implies that the expectation is ##0##. If we take two infinitesimal intervals ##[-x-dx, x]## and ##[x,x+dx]## on the wall, corresponding to the angle intervals ##[-\theta-d\theta, \theta]## and ##[\theta,\theta+d\theta]##, respectively, both having probability ##d\theta/\pi##, their contributions to the expectation are ##-xd\theta/\pi## and ##xd\theta/\pi##, respectively, so they cancel each other out. Every infinitesimal interval has such a "mirror" interval on the other side of ##a##, so the expectation must be ##0##.
How could it be in any other way?
So is it just an indeterminate form, like in my post #75 above?micromass said:Then by that same reasoning, would you say that ##\int_{-\infty}^{+\infty} xdx = 0## too?
TeethWhitener said:So is it just an indeterminate form, like in my post #75 above?
Yes, Ok, I agree. The integral ##\int_{-\pi/2}^{\pi/2}\tan\theta d\theta## diverges. Sorry...micromass said:Yes, the expectation value doesn't exist.
Erland said:So the entire problem was a poser...
Good point. I was assuming that ##E[X]=0##. Call it the "renormalized" answerErland said:But then, the variance is undefined also
Shreyas Samudra said:https://mail.google.com/mail/u/0/?u...68608010&rm=15794b3f1927dbe0&zw&sz=w1366-h662
https://mail.google.com/mail/u/0/?ui=2&ik=8afd5aa52a&view=fimg&th=15794b3f1927dbe0&attid=0.1&disp=inline&realattid=1547350341991792640-local0&safe=1&attbid=ANGjdJ9AL_gRE5sXmUYaevAhKSEVWeCDGMrM2iIlWdWoI_HQXuUtcdRj5gRNTsNVhx1fD7uUlFXVMOekFVnhgzPXCNVO8-rWTr1U5G2r1pmTcTPjii6g4adAZZBM6Ic&ats=1475668608010&rm=15794b3f1927dbe0&zw&sz=w1366-h662
Is it right ??
Shreyas Samudra said:
micromass said:CHALLENGES FOR HIGH SCHOOL AND FIRST YEAR UNIVERSITY:
Yes, and we've removed it.jostpuur said:Whoops... Did that mean that I should not have posted that answer?
I finally got the integral in the parameteric equation for y. @fresh_42 submitted the integrand to Wolfram Alpha, and it provided the closed-form result. Thanks you so much @fresh_42. Here is the desired result:Chestermiller said:My solution to this problem for x vs y, expressed parametrically in terms of ##\theta## is as follows:
$$x=x_0\left[1-\frac{1}{(\sec{\theta}+\tan{\theta})^{V/v}}\right]$$
$$y=x_0\left[\int_0^{\theta}{\frac{\sec^2{\theta '}d\theta '}{(\sec{\theta '}+\tan{\theta '})^{V/v}}}-\frac{\tan {\theta}}{(\sec{\theta}+\tan{\theta})^{V/v}}\right]$$where ##\theta '## is a dummy variable of integration.
Charles, your analytic solution to this problem should match mine, and should thus somehow provide the result of correctly integrating of my "mystery integral" in the equation for y. Could you please see if you can back out the integral evaluation? Thanks.
Chet
MAGNIBORO said:problem 4 highshool:
x coordinate = ##-1+\frac{1}{2}-\frac{1}{4}... = -1 + \frac{1}{2}(1-\frac{1}{2}+\frac{1}{3}...) = -1 + \frac{log(2)}{2}##
y coordinate = ##1-\frac{1}{3}+\frac{1}{5}..=\frac{\pi }{4}##
converges to the point ##\left ( -1+\frac{log(2)}{2},\frac{\pi }{4} \right )##
my mistake,micromass said:Read the problem more carefully. The lengths are defined recursive.
Hey i got the answer to the second of these questions, please tell me it is solved or unslovedparshyaa said:CHALLENGES FOR HIGH SCHOOL AND FIRST YEAR UNIVERSITY:
1) let A,B,C,D be a complex numbers with length 1. Prove that if A+B+C+D=0, then these four numbers form a rectangle.
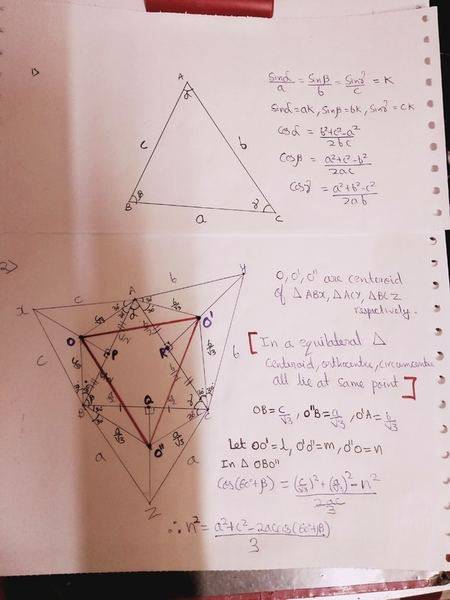
2) On an arbitrary triangle, we produce on each side an equilateral triangle. Prove that the centroids of these three triangles forms an equilateral triangle
- Are they unsolved
It means they are unsloved, thanksmfb said:If they are not marked as solved (and if the last 2-3 posts don't cover them), then no one posted a solution yet.
@micromassparshyaa said: