- #1
Karol
- 1,380
- 22
Homework Statement
Homework Equations
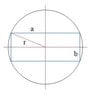
Pitagora's: ##~a^2+b^2=c^2##
Maxima/minima are where the first derivative is 0
The Attempt at a Solution
$$\left( \frac{a}{2} \right)^2+\left( \frac{b}{2} \right)^2=r^2~\rightarrow~b^2=\frac{16r^2}{a^2}$$
The strength S has the proportion coefficient k: ##~S=kab^2##
$$s=kab^2=k\frac{16r^2}{a^2}$$
$$S'=-16kr^2\dfrac{1}{a^2}$$
I can't equal this to 0
Attachments
Last edited by a moderator:


 )
)