Mapping Circles in the Complex Plane: A Conformal Approach

[CAF123]

Homework Statement

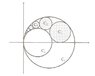
Consider two unshaded circles ##C_r## and ##C_s## with radii ##r>s## that touch at the origin of the complex plane. The shaded circles ##C_1,C_2...C_7## (labeled in counterclockwise direction sequentially) all touch ##C_r## internally and ##C_s## externally. ##C_1## also touches the real axis and ##C_i## and ##C_{ i+1}## touch for ##i=1...6##.

Let ##r_i## denote the radius of ##C_i##. Then show that for ##i=1,2..., ## $$r_i^{-1} + 3r_{i+2}^{-1} = 3r_{i+1}^{-1} + r_{i+3}^{-1}.$$
See picture attached.

Homework Equations

Inversions in the Complex plane

The Attempt at a Solution

I do not really see how to begin this problem and how it may be solved via methods from a Complex Analysis course. I was thinking initially to express the radii in the plane, but then this does not seem to help because it looks difficult to obtain an expression for the circles ##C_4..C_7## given the diagram. We are studying inversion in the complex plane, so that is why I put it in the relevant equations subsection, but I do not see why/if this helps. I then thought about induction since ##i## is an integer, but then to prove the base case would require knowledge of the radii of the circles.
Thanks for any hints.

 

[kduna]

I haven't tried to work through the problem, but I think this should help:

Consider the map [tex] f(z) = \frac{1}{z} [/tex] which is conformal. Thus it maps circles in the plane to circles or lines in the plane. Try finding the images of those circles under f. Working with the resulting lines should be much easier.

 

[CAF123]

Hi kduna,
It is clear that circles ##C_r## and ##C_s## are mapped to lines under the transformation and that ##C_i## for ##i \in \left\{1,...,6\right\}## are mapped to circles. Since the map is conformal, the angles in the plane are preserved where ##f'(z)## is defined. Each circle has 4 tangent points and thus there are 4 ##\pi/2## angles preserved.

Taking this into account, the radius I got for circle ##C_i##under the transformation is the same for all ##i##, namely ##1/4s##, where ##s## is the radius of ##C_s##. I am not really sure if this makes sense, but at the same time, I do not see how else the circles would get mapped in order to preserve all four angles.

Thanks.

Edit: defined notation more.