- #1
SprucerMoose
- 62
- 0
G'day,
I'm just doing some physics homework and decided to attempt to prove something. This is not a homework problem, I'm just unsure how to evaluate the limit.
Using the equation for transformation of velocity U=(U'+V)/(1+(VU'/c2)), I'm trying to show that if V=-c, as U' approaches c, U should approach c. This is the case when something travels at c in one direction and shines a light in the opposite direction, to an observer on the ground, where U will still be c.
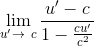
I'm just doing some physics homework and decided to attempt to prove something. This is not a homework problem, I'm just unsure how to evaluate the limit.
Using the equation for transformation of velocity U=(U'+V)/(1+(VU'/c2)), I'm trying to show that if V=-c, as U' approaches c, U should approach c. This is the case when something travels at c in one direction and shines a light in the opposite direction, to an observer on the ground, where U will still be c.