Instantaneous moment of inertia of an object

[Bolter]

Homework Statement

Work out the instantaneous moment of inertia and show that the length of the string that wound around the peg is 1.40 m when v = 20 m/s

Relevant Equations

rotational equivalent of SUVAT eqns

Can someone guide me on how to approach this question?

I tried to draw a quick diagram of what I think is happening here

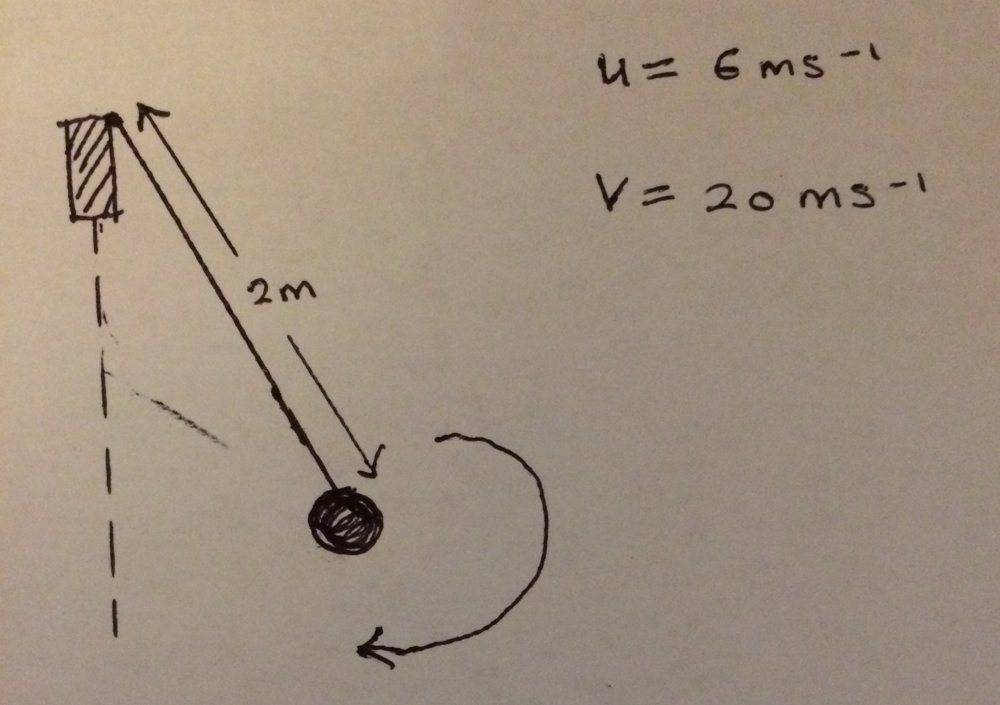
Does the question imply that this object is undergoing horizontal circular motion in the shape of a conical pendulum?

Thanks for any help!

 

[haruspex]

Does the question imply that this object is undergoing horizontal circular motion in the shape of a conical pendulum?

Almost, but the radius will decrease.

 

[Bolter]

Almost, but the radius will decrease.

Alright I see. Does resolving the forces that act on the object helpful in finding moment of inertia?

I also tried this, but I cannot get moment of inertia as I do not know torque, radius nor linear acceleration.

 

[haruspex]

Moment of inertia of a point particle about a given axis is very simple. It's just mr².

But I am bothered by this question. Where is all that extra KE coming from?
The only reason the string gets shorter is that the peg has some thickness, and that means the tension exerts a torque about the central axis of the stick. The question setter seems to expect you to use conservation of angular momentum, but I feel it is not justified.

To make it simpler, ignore gravity and take the motion all to be in one plane, string included. This means work is conserved. If the stick has radius r and the string length is R(t) then I get that the speed, v, is constant and R²=R₀²-2vrt.

Where did you find this question?

 

[Bolter]

It was a homework sheet that my teacher had set me so I have no idea where it came from

Okay so if they could be expecting me to use conservation of angular momentum. I know that as the string gets wrapped around the peg, radius gets smaller thus the angular velocity must increase for angular momentum to be conserved.

However when I set up the equation. I see that I get 2 different angular velocities on either side, hence I deal with 2 different linear speeds and radius lengths. How would I go about this then?

I tried viewing this scenario in birds eye view, so looking down at the object from above where the dot in the centre represents the central axis. This would be one way looking at the motion in a one dimensional manner.

Also how did you come to getting the equation \rm{R^2} = \rm{R_0^2} – 2vrt? I'm a bit still confused on that part.

 

[haruspex]

It was a homework sheet that my teacher had set me so I have no idea where it came from

Okay so if they could be expecting me to use conservation of angular momentum. I know that as the string gets wrapped around the peg, radius gets smaller thus the angular velocity must increase for angular momentum to be conserved.

However when I set up the equation. I see that I get 2 different angular velocities on either side, hence I deal with 2 different linear speeds and radius lengths. How would I go about this then?

I tried viewing this scenario in birds eye view, so looking down at the object from above where the dot in the centre represents the central axis. This would be one way looking at the motion in a one dimensional manner.

View attachment 254615

You have not used what I told you about angular momentum of point particles.
The I will change too.
In fact, for point particles you don't need I, you can just use linear momentum x perpendicular distance.
If v and r are orthogonal, ##I\omega=mr^2\omega=mvr##

 

[kuruman]

Here is the figure accompanying my interpretation of the problem. It shows a bird's eye view of mass ##m## sliding on a horizontal frictionless plane at the end of a string of total length ##L## (red line). Angular momentum is not conserved about the center axis of the peg (point O) but is conserved about the point where the string loses contact with the peg (point A).

I would assume that the problem is asking for the instantaneous moment of inertia ##I_O=mr^2## about point O as a function of time.

 

[haruspex]

how did you come to getting the equation ##m{R^2} = m{R_0^2} – 2vrt##?

Conservation of mechanical energy means the speed is constant. Tension is ##\frac{mv^2}R##. This exerts a torque ##r\frac{mv^2}R## about the central axis. The particle's angular momentum about that axis is ##mvR##, so ##mv\dot R=-r\frac{mv^2}R##. Solve.

 

[haruspex]

Here is the figure accompanying my interpretation of the problem. It shows a bird's eye view of mass ##m## sliding on a horizontal frictionless plane at the end of a string of total length ##L## (red line). Angular momentum is not conserved about the center axis of the peg (point O) but is conserved about the point where the string loses contact with the peg (point A).

I would assume that the problem is asking for the instantaneous moment of inertia ##I_O=mr^2## about point O as a function of time.

View attachment 254619

The question makes no mention of sliding on a horizontal plane, so I think the diagram in post #1 is a correct interpretation. That said, it makes the problem quite complicated because it is far from obvious what the vertical motion of the particle will be.

The question setter has blundered anyway by a) assuming angular momentum is conserved and b) ignoring that KE should be at least approximately conserved. So I have no difficulty believing the issue of vertical motion was also overlooked.

According to my analysis in post #8, the tension should increase, leading to the string getting closer to horizontal. That will make the particle rise a little, robbing it of some KE.

 

[kuruman]

The question makes no mention of sliding on a horizontal plane, so I think the diagram in post #1 is a correct interpretation.

Are you saying that we have a conical pendulum in which case my diagram in #7 is a projection in the horizontal plane?

 

[Bolter]

You have not used what I told you about angular momentum of point particles.
The I will change too.
In fact, for point particles you don't need I, you can just use linear momentum x perpendicular distance.
If v and r are orthogonal, ##I\omega=mr^2\omega=mvr##

I see how this was obtained and how it equals to the moment of inertia. However I only know the linear speed here which is known to be 6 m/s . I cannot see how I will be able to work out mass or the radius length from the info given in the question? I'm struggling to see how these other unknowns are found...

 

[haruspex]

Are you saying that we have a conical pendulum in which case my diagram in #7 is a projection in the horizontal plane?

Yes, except it is only really valid to reduce it to its projection in the horizontal plane if the particle's trajectory lies in such. As I posted, I believe in practice it will rise a little as the radius reduces.

 

[haruspex]

I see how this was obtained and how it equals to the moment of inertia. However I only know the linear speed here which is known to be 6 m/s . I cannot see how I will be able to work out mass or the radius length from the info given in the question? I'm struggling to see how these other unknowns are found...

The mass is irrelevant. As often happens, you can just set that to some unknown and it will cancel out later.
Likewise, for the method the question setter intends you to use, the actual radii don't matter. You just have to assume the string makes a constant angle to the vertical, so the ratio of radius to remaining straight section of string is constant.

But as I hope I have explained, the question is unanswerable. The speed will not increase, so can never reach 20m/s.

 

[Bolter]

The mass is irrelevant. As often happens, you can just set that to some unknown and it will cancel out later.
Likewise, for the method the question setter intends you to use, the actual radii don't matter. You just have to assume the string makes a constant angle to the vertical, so the ratio of radius to remaining straight section of string is constant.

But as I hope I have explained, the question is unanswerable. The speed will not increase, so can never reach 20m/s.

Is this what you mean when you say the mass is irrelevant so cancels out? I got the ratio of the radius to be equal some ratio of the speeds.

 

[haruspex]

Is this what you mean when you say the mass is irrelevant so cancels out? I got the ratio of the radius to be equal some ratio of the speeds.

View attachment 254624

Yes, that seems to be what the question setter has done (erroneously).

 

[Bolter]

Yes, that seems to be what the question setter has done (erroneously).

Then subbing the values I need from the Q, I get r_2 to be 0.6m. So the length that gets wounded around the peg is 2m – r_2 = 1.4m

But I still cannot see why mass does not need to be used to find moment of inertia? Both I = mr^2 and and I = angular momentum/ angular velocity both involve a m in the equation. I can't see where m cancels out

 

[kuruman]

Yes, that seems to be what the question setter has done (erroneously).

The numerical answer of 1.40 m can be obtained under the assumption that the motion takes place in a horizontal plane as indicated in post #7. The charitable interpretation (it's Christmas season after all) would be that the question setter acted negligently rather than erroneously.

 

[gneill]

The question does not explicitly say that the string and object form a conical pendulum. It could well be that the object is moving on a horizontal frictionless surface, where the string is winding around a spindle. Yes, the question as posed is annoyingly vague.

 

[haruspex]

I can't see where m cancels out

In the image you posted in #14 there is an equation with a crossed out m each side. Looks like cancellation to me.

 

[haruspex]

The numerical answer of 1.40 m can be obtained under the assumption that the motion takes place in a horizontal plane as indicated in post #7. The charitable interpretation (it's Christmas season after all) would be that the question setter acted negligently rather than erroneously.

No, no! You are missing the major blunder, which still applies in the smooth plane interpretation. Angular momentum is not conserved, kinetic energy is conserved, the speed is constant, the quoted 20m/s will never be reached.
No Christmas cheer absolves that one.

 

[kuruman]

In the smooth plane interpretation, the torque about point A in the diagram (post #7) is zero. Does that not mean that the angular momentum about point A obeys ##\frac{d\vec L_{A}}{dt}=0~##? If so and because point A is arbitrary, angular momentum about the instantaneous point of making contact is conserved. That is the key to the answer.

It is also interesting to note that the angular momentum about the center O is equal to the angular momentum about A. That's because ##\vec r=\vec{OA}+\vec {d}## where ##\vec d## is the vector from A to the mass. Now ##\vec L_O=\vec r \times \vec p= (\vec{OA}+\vec {d})\times \vec p=\vec{OA}\times \vec p+\vec d\times \vec p=\vec d\times \vec p=\vec L_A.## Note that ##\vec{OA}\times \vec p=0## because the two vectors are antiparallel as seen in the drawing.

I am not sure that kinetic energy is conserved. The tension has a radial component (towards point O). As the mass is pulled towards the center, the tension does positive work on the mass and the kinetic energy increases.

 

[haruspex]

In the smooth plane interpretation, the torque about point A in the diagram (post #7) is zero. Does that not mean that the angular momentum about point A obeys ##\frac{d\vec L_{A}}{dt}=0~##? If so and because point A is arbitrary, angular momentum about the instantaneous point of making contact is conserved. That is the key to the answer.

It is also interesting to note that the angular momentum about the center O is equal to the angular momentum about A. That's because ##\vec r=\vec{OA}+\vec {d}## where ##\vec d## is the vector from A to the mass. Now ##\vec L_O=\vec r \times \vec p= (\vec{OA}+\vec {d})\times \vec p=\vec{OA}\times \vec p+\vec d\times \vec p=\vec d\times \vec p=\vec L_A.## Note that ##\vec{OA}\times \vec p=0## because the two vectors are antiparallel as seen in the drawing.

I am not sure that kinetic energy is conserved. The tension has a radial component (towards point O). As the mass is pulled towards the center, the tension does positive work on the mass and the kinetic energy increases.

Applying conservation of angular momentum about an axis that keeps shifting is fraught. Very easy to fall into error.
Taking the fixed axis O is quite safe, and you can see that the tension exerts a retarding torque about that axis.

The tension does no work, though. The motion of the particle is always normal to the tension. (If it were to do positive work, where would it be getting that from?)

 

[kuruman]

No, no! You are missing the major blunder, which still applies in the smooth plane interpretation. Angular momentum is not conserved, kinetic energy is conserved, the speed is constant, the quoted 20m/s will never be reached.
No Christmas cheer absolves that one.

I missed the major blunder perhaps because it is major enough to hide in plain sight. Thank you for being charitable with me. 'Tis the season ...

 

[haruspex]

I missed the major blunder perhaps because it is major enough to hide in plain sight. Thank you for being charitable with me. 'Tis the season ...

Enjoy.

 

[Bolter]

In the image you posted in #14 there is an equation with a crossed out m each side. Looks like cancellation to me.

Yes but that is for when I was dealing with angular momentum. If I want to give the instantaneous moment of inertia at the beginning, I see I=mr^2 where r =2 m? So my I = m(2)^2 = 4m. This doesn't seem like a complete value to give :(

 

[haruspex]

Yes but that is for when I was dealing with angular momentum. If I want to give the instantaneous moment of inertia at the beginning, I see I=mr^2 where r =2 m? So my I = m(2)^2 = 4m. This doesn't seem like a complete value to give :(

Ah, ok.
No, you do not have the mass, and if the conical pendulum interpretation is correct you do not have the radius either. So you can only express the MoI in abstract form.

 

[kuruman]

The tension does no work, though. The motion of the particle is always normal to the tension. (If it were to do positive work, where would it be getting that from?)

Well, I investigated this (motion on frictionless horizontal plane) a bit more and derived the equation of motion using the Lagrangian method which I trust better than my assumptions about this problem. I started formally with Cartesian coordinates relative to the center, wrote down ##\dot x^2+\dot y^2## subject to the constraint ##L=s+R\theta## where L is the constant length of the string, ##R## is the radius of the peg and ##s## is the taut straight length of the string. The kinetic energy turns out to be $$K=\frac{1}{2}m(L-R\theta)^2\dot \theta^2.$$Here, ##\theta## is the angle between the instantaneous and the initial direction of the taut string. Note that this term is the rotational kinetic energy about the point where the string loses contact with peg and this makes sense. There is no potential energy term therefore the kinetic energy is the Lagrangian. The ensuing equation of motion is$$(L-R\theta)^2\ddot \theta=0.$$This implies that ##\dot \theta=\text{const.}=\omega.## At ##t=0##, ##s=L## and the mass is given initial velocity ##v_0## perpendicular to the string that is held taut. Then ##\dot \theta(0)=\omega=\dfrac{v_0}{L}## and $$K=\frac{1}{2}m v_0^2\left(1-\frac{R\theta}{L}\right)^2.$$The kinetic energy is not constant but changes from its initial value to zero when the string is fully wrapped at ##\theta=L/R##. So where does the kinetic energy go?

The tension is $$T=m\omega^2(L-R\theta)=\frac{m v_0^2}{L}\left(1-\frac{R \theta}{L}\right).$$ The straight segment of the string (length ##s##) is getting shorter as the mass goes around. The tension ##\vec T## and the change in length ##d\vec s## are in the same direction. Consider ##dW=\vec T\cdot d\vec s=T~ds =Td(L-R\theta)=-TRd\theta## and evaluate the suggested integral, $$W=\int T~ds=-\frac{m v_0^2}{L}\int_0^{L/R} \left(1-\frac{R \theta}{L}\right) R d\theta=-\frac{1}{2}mv_0^2.$$This last result is consistent with the work-energy theorem ##\Delta K=W##.

 

[haruspex]

The ensuing equation of motion is ##(L−R\theta)^2\ddot \theta=0##

I think you've dropped a factor 1/2 in your differentiation of L wrt theta. I get ##(L−R\theta)^2\ddot \theta=(L-R\theta)\dot\theta^2R##, whence ##(L−R\theta)\ddot \theta=\dot\theta^2R##, which has the solution ##(L−R\theta)\dot \theta=const##, matching my own analysis.

I never studied or worked with Langrangians before, so you had me stuck for a while, but I really could not see how this system could be other than work conserving.
Having been made to read up on it, I experimented with the general case of ##L=r^m\dot r^n##. It gives ##m\dot r^2+nr\ddot r=0##. When m=n, as here, ##\dot r^2+r\ddot r=0##.

 

[kuruman]

I think you've dropped a factor 1/2 in your differentiation of L wrt theta.

I think so too. Thanks for the reality check.