- #1
Kastenfrosch
- 6
- 0
Hello!
The incompressible Navier Stokes equation consists of the two equations
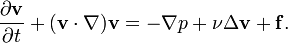
and
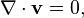
Why can't i insert the 2nd one into the first one so that the advection term drops out?!
[tex]\nabla\cdot[/tex]v = v[tex]\cdot\nabla[/tex] = 0
=>
(v[tex]\cdot\nabla)\cdot[/tex]v = 0
The incompressible Navier Stokes equation consists of the two equations
and
Why can't i insert the 2nd one into the first one so that the advection term drops out?!
[tex]\nabla\cdot[/tex]v = v[tex]\cdot\nabla[/tex] = 0
=>
(v[tex]\cdot\nabla)\cdot[/tex]v = 0
Last edited by a moderator:
