How to derive the frequency for two body oscillatory motion

[Tony Hau]

Homework Statement

Two masses 𝑚1 = 100g and 𝑚2 = 200g slide freely in a horizontal frictionless track and are
connected by a spring whose force constant is 𝑘 = 0.5 N/m. Find the frequency of the
oscillatory motion of the system. [Hint: write down the equation of motion of each mass in
the center of mass frame]

Relevant Equations

m2(x2) = -kΔ(x2)
m1(x1)=-kΔ(x1)

Here is the diagram of the problem:

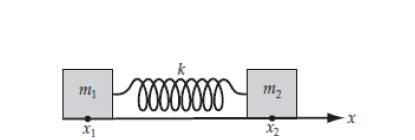
and here is the answer of the question:

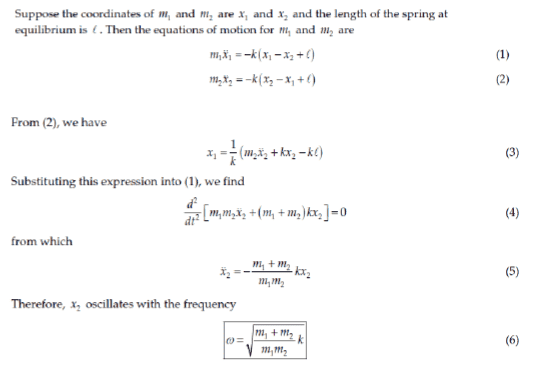
What I don't understand is equation 1 and 2.
The Hook's law states that F = -k(change in x)
Why the change in x1 equals to x1-x2+l? x1-x2 equals to the length of the compressed spring. I cannot convince myself that the length of the compressed spring plus the length of the uncompressed spring equals to the change in x1.

 

[BvU]

x1-x2 equals to the length of the compressed spring

Doesn't look like that !

 

[BvU]

Hook's law states that F = -k(change in x)

Only if someone tells us what ##x## is !

 

[Cutter Ketch]

x1-x2 equals to the length of the compressed spring.

x1 and x2 are the positions of the 2 masses as a function of time. These are changing all the time. That isn’t the length of the compressed spring (or the uncompressed spring) that is the length of the spring at any moment. (The whole solution takes the masses as having no width, but that is fine as any width just gets incorporated into l and you can call l the positions when the spring is at equilibrium rather than the length of the spring at equilibrium)

The length of the spring at any moment x1-x2 (or with just a change of sign x2-x1) minus the equilibrium length l is how far the spring is stretched or compressed at any moment. This is the x that goes into Hooke’s law. Equations 1 and 2 are simply Hooke’s law with the appropriate sign change for which direction each mass is being pulled.

 

[Tony Hau]

Only if someone tells us what ##x## is !

I am confused, can you explain more?

 

[Tony Hau]

x1 and x2 are the positions of the 2 masses as a function of time. These are changing all the time. That isn’t the length of the compressed spring (or the uncompressed spring) that is the length of the spring at any moment. (The whole solution takes the masses as having no width, but that is fine as any width just gets incorporated into l and you can call l the positions when the spring is at equilibrium rather than the length of the spring at equilibrium)

The length of the spring at any moment x1-x2 (or with just a change of sign x2-x1) minus the equilibrium length l is how far the spring is stretched or compressed at any moment. This is the x that goes into Hooke’s law. Equations 1 and 2 are simply Hooke’s law with the appropriate sign change for which direction each mass is being pulled.

I got your point. But how should I understand the Hooke's Law in this case? I thought that the change in x in the Hooke' Law equals to 0.5l-(x-the x of centre of mass). Basically what I think is that the x of the centre of mass is not changing. So we find the distance from x to the centre of mass. Then we minus it with the distance from the unstreched end to the centre of mass. Here we get the change in x.

 

[BvU]

I am confused, can you explain more?

Apparently. Your "change in x" in "F = -k(change in x) " requires definition. Something like "length minus length in the state with F = 0".

In the picture ##x_2 > x_1## clearly. So ##x_1-x_2 < 0## and the spring is relaxed (F=0) when ##x_1-x_2 + {\mathcal l} = 0## .

With ##x_1-x_2 + {\mathcal l} < 0##, for example when ##x_1## stays the same and ##x_2## is increased, the spring will pull to the right on ##m_1##, i.e. ##\ddot x_1>0##.

Conclusion: ##m_1\ddot x = -k(x_1-x_2 + {\mathcal l} )## is the correct expression for ##m_1##.

@Tony Hau: Can you now do the same reasoning for to get an expression for ##m_2## ?

Note: there is a typo in (2) -- and (3) is correct -- I now understand your confusion.

 

[Cutter Ketch]

I got your point. But how should I understand the Hooke's Law in this case? I thought that the change in x in the Hooke' Law equals to 0.5l-(x-the x of centre of mass). Basically what I think is that the x of the centre of mass is not changing. So we find the distance from x to the centre of mass. Then we minus it with the distance from the unstreched end to the centre of mass. Here we get the change in x.

By Hooke’s law it requires a force = -kx to stretch a spring by x. However that only describes the force at one end. We usually think of the spring as being attached to a wall or something. But really that is also the force at the other end of the spring. You can’t stretch a spring by applying a force to only one end! So the Hooke’s law force has to be applied at both ends of the spring. In this case there are masses at both ends. They must experience equal and opposite forces and the force they experience is kx. If the spring is stretched x one feels a force of kx toward the left and the other feels a force of kx to the right.

 

[Tony Hau]

By Hooke’s law it requires a force = -kx to stretch a spring by x. However that only describes the force at one end. We usually think of the spring as being attached to a wall or something. But really that is also the force at the other end of the spring. You can’t stretch a spring by applying a force to only one end! So the Hooke’s law force has to be applied at both ends of the spring. In this case there are masses at both ends. They must experience equal and opposite forces and the force they experience is kx. If the spring is stretched x one feels a force of kx toward the left and the other feels a force of kx to the right.

Thanks for you reply. It is much clearer than what is written on textbooks.

 

[Tony Hau]

Apparently. Your "change in x" in "F = -k(change in x) " requires definition. Something like "length minus length in the state with F = 0".

In the picture ##x_2 > x_1## clearly. So ##x_1-x_2 < 0## and the spring is relaxed (F=0) when ##x_1-x_2 + {\mathcal l} = 0## .

With ##x_1-x_2 + {\mathcal l} < 0##, for example when ##x_1## stays the same and ##x_2## is increased, the spring will pull to the right on ##m_1##, i.e. ##\ddot x_1>0##.

Conclusion: ##m_1\ddot x = -k(x_1-x_2 + {\mathcal l} )## is the correct expression for ##m_1##.

@Tony Hau: Can you now do the same reasoning for to get an expression for ##m_2## ?

Note: there is a typo in (2) -- and (3) is correct -- I now understand your confusion.

Is it ##m_2\ddot x = -k(x_2-x_1 - {\mathcal l} )## for the equation 3?
It is because when x2 -x1-l<0, the spring is compressed and the acceleration of mass 2 is positive,directed towards the right.

 

[Tony Hau]

One last question: I am confused with equation 5. What does that x2 on the right hand side mean? x2 is not the difference between the unstretched and stretched spring in this equation. It is simply the coordinate of x2. In that case, x2 is always positive as shown in the diagram. That means that the acceleration of x2 is always negative, directed towards the left. It doesn't make sense.

 

[haruspex]

One last question: I am confused with equation 5. What does that x2 on the right hand side mean? x2 is not the difference between the unstretched and stretched spring in this equation. It is simply the coordinate of x2. In that case, x2 is always positive as shown in the diagram. That means that the acceleration of x2 is always negative, directed towards the left. It doesn't make sense.

Equation 5 is obtained from equation 4 by two integrations. Each should introduce an unknown constant to be resolved using boundary conditions. The author seems to have forgotten this in the second integration.
Have a go at doing it correctly.

 

[SammyS]

Is it ##m_2\ddot x = -k(x_2-x_1 - \ell )## for the equation 3?
It is because when x2 -x1-l<0, the spring is compressed and the acceleration of mass 2 is positive,directed towards the right.

Actually that's the corrected version of Eq. (2).

 

[ehild]

The masses are connected to the ends of the same spring, so they ave subjected to forces of the same magnitude and opposite direction. x1 is the position of m1 and x2 is that of m2. The length of the spring os x2-x1, and the magnitude of the spring force is F=k(x2-x1-Lo). When the spring is stretched, this force pulls both masses towards the CM, and it pushes them apart, when the spring is compressed.

If m1 moves to the right, the spring pushes it backward, and pushes m2 forward., to the positive x direction. . When m2 moves to the right, the spring pulls m1 to the right and m2 to the left.

According to Newton's Second Law,
##\ddot x_1=\frac{k}{m_1}(x_2-x_1-L_o)## (1)
##\ddot x_2= -\frac{k}{m_2}(x_2-x_1-L_o)## (2)
Subtract (1) from(2):
##\ddot x_2-\ddot x_1=-k(\frac{1}{m_1}+\frac{1}{m_2})(x_2-x_1-L_o)## (3)
Introduce the variable u=x2-x1-Lo, ,the change of length of the spring,.

 

[Cutter Ketch]

In that case, x2 is always positive as shown in the diagram. That means that the acceleration of x2 is always negative, directed towards the left. It doesn't make sense.

Yes the right hand mass stays on the right hand side, but it moves left and right as the spring vibrates. It starts out toward the left. Eventually it reaches the equilibrium point of the spring. However, by that point it has accumulated momentum. It moves through the equilibrium point and starts to compress the spring. Now the spring is pushing to the right. The force and the acceleration are now to the right. The force decelerates the mass until it stops and turns around. However by that time the spring is compressed, so it starts accelerating the mass back to the right. And you can see that the system oscillates.

 

[Tony Hau]

Yes the right hand mass stays on the right hand side, but it moves left and right as the spring vibrates. It starts out toward the left. Eventually it reaches the equilibrium point of the spring. However, by that point it has accumulated momentum. It moves through the equilibrium point and starts to compress the spring. Now the spring is pushing to the right. The force and the acceleration are now to the right. The force decelerates the mass until it stops and turns around. However by that time the spring is compressed, so it starts accelerating the mass back to the right. And you can see that the system oscillates.

Crystal clear, thanks!

 

[Tony Hau]

The masses are connected to the ends of the same spring, so they ave subjected to forces of the same magnitude and opposite direction. x1 is the position of m1 and x2 is that of m2. The length of the spring os x2-x1, and the magnitude of the spring force is F=k(x2-x1-Lo). When the spring is stretched, this force pulls both masses towards the CM, and it pushes them apart, when the spring is compressed.
View attachment 259956If m1 moves to the right, the spring pushes it backward, and pushes m2 forward., to the positive x direction. . When m2 moves to the right, the spring pulls m1 to the right and m2 to the left.

According to Newton's Second Law,
##\ddot x_1=\frac{k}{m_1}(x_2-x_1-L_o)## (1)
##\ddot x_2= -\frac{k}{m_2}(x_2-x_1-L_o)## (2)
Subtract (1) from(2):
##\ddot x_2-\ddot x_1=-k(\frac{1}{m_1}+\frac{1}{m_2})(x_2-x_1-L_o)## (3)
Introduce the variable u=x2-x1-Lo, ,the change of length of the spring,.

The spring constant in this case becomes k(m1+m2) and the mass becomes m1*m2.

 

[SammyS]

The spring constant in this case becomes k(m1+m2) and the mass becomes m1*m2.

It's true that, ##\ \ k\left(\dfrac1{m_1}+\dfrac1{m_2}\right) = \dfrac{k\left(m_1+m_2\right)}{m_1 m_2}##, and comparing that with ##\dfrac k m ##, your conclusion looks reasonable ... except for the units. A spring constant should not have units of N⋅kg/m and mass should not have units of kg².

Instead, think of that as ##\displaystyle \frac{k}{\left(\dfrac{m_1 m_2}{m_1+m_2}\right)} \ \ .##

OR ... Using m for either of the masses and M for the other you can think of this system as having an altered mass with the given spring constant or as an altered spring constant with either mass. Rewrite your expression (for ω² ) as any of the following.

##\displaystyle \dfrac{k}{m\left(\dfrac{ M}{m+M}\right)} \ \ ##

##\displaystyle \dfrac {k \left( \dfrac{ m+M}{M } \right) }{m}\ \ ##