- #1
smr101
- 72
- 0
I can't work out the strain energy using the integral equation here, question (b)(i).
I've got the bending moment for the first beam as 400kN.
E and I are given, I'm guessing you can take '2EI' out of the integral and just integrate the M^2, is that correct?
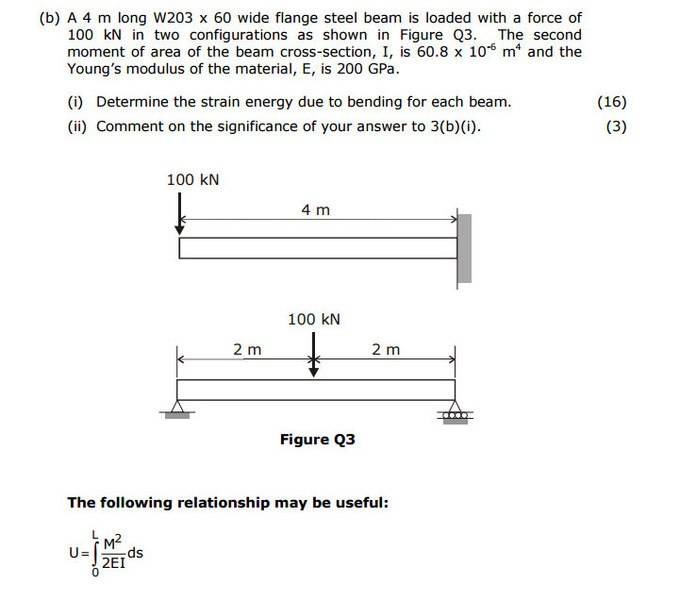
I've got the bending moment for the first beam as 400kN.
E and I are given, I'm guessing you can take '2EI' out of the integral and just integrate the M^2, is that correct?