How do i determine the final position?

[cshum00]

So i made up this simple setup:

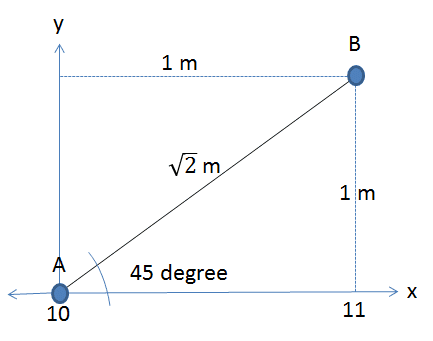
I have a √(2) meter stick slanted on a friction-less surface on a 45° angle. And i want to determine the final x and y positions of the points A and B.

For point A:
A.1) Solving for a_x
[tex]\sum F_x = T_x = F_x[/tex][tex]Tcos(\theta) = ma_x[/tex][tex]a_x = \frac{Tcos(\theta)}{m}[/tex]

A.2) a_y=0. It is zero because the surface does not allow point A to move downward.

For point B:
B.1) a_x is the same as point A because both move on the x-axis at the same rate.

B.2) Solving for a_y
[tex]\sum F_y = T_y - F_g = F_y[/tex][tex]Tsin(\theta) - mg = ma_y[/tex][tex]a_y = \frac{Tsin(\theta)}{m} - g[/tex]

Then how do i compile these accelerations into the kinematic equations? Assuming that:
-The initial velocity v₀=0 for both axis and points
-The initial position of point A is A₀(x,y)= (10,0)
-The initial position of point B is B₀(x,y)= (11,1)
-The initial angle θ₀=45

I know that θ is my variable since the angle will become smaller all the way to zero. But i also see that the tension T on the stick also varies with the angle. So i have no idea how to move from here.

 

[NascentOxygen]

Are A and B the end points on a uniform stick, or are they weights attached to the ends of a weightless stick?

 

[cshum00]

A uniform stick. Then does it mean i have to calculate the center of mass and gravity? If so how do i relate the center of mass to point A and B?

 

[NascentOxygen]

A uniform stick. Then does it mean i have to calculate the center of mass and gravity? If so how do i relate the center of mass to point A and B?

The C of M of a uniform rod is its midpoint.

 

[NascentOxygen]

This would be a good candidate for an experiment. Use the handle of a broom or rake, and rest one end on a couple of pieces of slippery baking paper. Drop the high end and record where it lands. See whether theory agrees with practice.

 

[Philip Wood]

No horizontal forces, then? ...

What, then, can be said about the horizontal motion of the centre of mass?

 

[cshum00]

@NascentOxygen
I am trying to get the numerical theory first. So i can't confirm anything the practice with at the mean time.

@Philip Wood
I think there is a horizontal force created by the tension of the stick. Otherwise the center of mass would not be connected to the stick but it would be free-falling like a single particle.

 

[tony873004]

Here's my guess:
There's no friction, so I don't see any horizontal forces acting on the system. Gravity pulls down. Normal force pushes up on point A creating a torque on the system. So the stick will simply rotate about its center of mass, with the center of mass dropping straight down on position x=10.5. Therefore, the x-position of point A will be 10-(√2)/2 and the x-position of point B will be 11+(√2)/2 . The y-positions of both A and B will be zero as the stick is lying on the table.

Trying the experiment as NascentOxygen suggested seems to confirm this, although no surface is truly frictionless. I just tried it with a pencil. I found the center of mass by balancing it on another pencil. I then drew a line. I then released it from several different angles. Each time, the COM ended up almost directly under its initial position.

 

[cshum00]

@tony873004
Experiment-wise i got similar results. Before and after dropping, the center of mass land closely to the initial position. But i still can't get it right algebraic-wise.

Also, it doesn't make sense to have no horizontal force for the following reasons:
-If point A is i contact with the surface and it can't go down; then there is a normal force pushing it up.
-If there is a normal force pushing the stick up; then there is definitely tension. You can even definitely get a vector component parallel to the stick (or vector parallel to the tension).
-And if there is tension, there is definitely a horizontal or x-component.

 

[Philip Wood]

There is some confusion here. Forces inside the stick, that is between one part of the stick and another, aren't relevant to the stick's motion. The only forces relevant to the stick's motion are those from outside the stick. In this case there are only two of these, and neither is horizontal!

 

[cshum00]

@Philip Wood
Then, how do i calculate the torque in this case? Normally to calculate the torque, i need a fixed pivot and a fixed tangent force times the radius. Here, although the radius to the center of mass is fixed; the pivot point and tangent force are not. Do you mind to help me elaborating?

 

[NascentOxygen]

The reaction at A is due to the moment of inertia of the rod as it is forced to rotate CW. The question asks for nothing more than the final position of the ends of the rod.

When I suggested a practical exercise, I was visualizing a timber cutter felling a tree. If the tree slips off its stump partway through the fall you see the tree "kick back" off the stump, so the guy with the chainsaw needs to move away quickly in case the tree becomes free to rotate about its C of M.

 

[cshum00]

@NascentOxygen
Well, the idea was to calculate the horizontal and vertical accelerations and formulate a kinematic equation. That way i could not only calculate the final position, but also the time, instant velocity, instant acceleration depending on the initial conditions given. Observation-wsie i have an idea of what is going to happen. But i want to be able to do the calculation.

 

[NascentOxygen]

The picture as I see it is that the C of M descends under free fall. From the geometry, you can determine the rotational speed of the beam in relation to the position/velocity of the beam. Knowing the rotational speed/acceleration of the beam, and the beam's moment of inertia, you can determine the vertical reaction at A.

 

[willie001]

This would be a good candidate for an experiment.http://www.amzcard.info/g.gif

 

[rcgldr]

If there is a normal force pushing the stick up; then there is definitely tension.

That would be an internal compressive force: the compressive force along the rod at any point on the rod is due to equal and opposing forces, the component of force originating from the frictionless surface, and the component of force originating from gravity ( m(g - a), where a is the rate of downwards acceleration of the C of M). It would be easiest to visualize this if the rod was vertical and not falling. Then the compressive force at any point on the rod would be related to the mass of the rod above that point times g.

The picture as I see it is that the C of M descends under free fall.

There's an upwards force from the frictionless surface at point A, so the acceleration of the C of M is less than 1 g.

Then, how do i calculate the torque in this case?

I'm not sure if you can treat gravity as acting at the midpoint of the rod, but if it can, then the torque force equals upwards force at A times horizontal component of distance from A to midpoint of rod (actually 1/2 horizontal component of distance to midpoint x (upwards force at A + downwards force at midpoint (these forces are equal and opposing))).

 

[cshum00]

The picture as I see it is that the C of M descends under free fall.

Here is why i am not so sure the center of mass "descends under free fall". Not all of the force is converted to horizontal forces at point A. The vertical forces canceled by the normal force at point A is sent back internally in the stick and converted into rotational force.

From the geometry, you can determine the rotational speed of the beam in relation to the position/velocity of the beam.

Let's make it simpler. There is no initial velocity. The stick is at rest at t=0. Then, can you show me geometry you are describing in algebraic from? I can't see that as i said before. I don't know how to calculate the torque when we don't have a fixed pivot and tangent force.

Knowing the rotational speed/acceleration of the beam, and the beam's moment of inertia, you can determine the vertical reaction at A.

I am assuming that you are referring to the Normal force when you say "vertical reaction at A". I can do that by analyzing the vertical forces at point A using the tension of the stick.[tex]\sum F_y = N - Tsin(\theta) = 0[/tex][tex]N = Tsin(\theta)[/tex][tex]T = Mgsin(\theta)[/tex][tex]N = Mgsin^2(\theta)[/tex]
So, N(θ=0°)=0 and N(θ=90°)=Mg. Which looks right to me.

That would be an internal compressive force

Yes and no. It a real situation, it is an internal compressible force. But in our case we don't like to call it that because it implies that the length of the stick can shorten. Also, to calculate compression, you need Force divided by Area. Our stick is one dimensional so we can't do that. And for simplicity, we want the stick to be incompressible. So we just call it tension.

I'm not sure if you can treat gravity as acting at the midpoint of the rod, but if it can, then the torque force equals upwards force at A times horizontal component of distance from A to midpoint of rod (actually 1/2 horizontal component of distance to midpoint x (upwards force at A + downwards force at midpoint (these forces are equal and opposing))).

I believe it is a typo in your side; the center of gravity is midpoint with no doubt. What we are not 100% so sure is whether it will fall down vertically. That is because we don't know if and how much the normal force will convert the tension into rotational force and shift the fall of the center of gravity.
But because there are no relevant external horizontal forces, we will try to assume that the conversion of the normal tension to rotational force will not shift the path of the center of gravity. Or better said, we will assume that the horizontal tension created by the normal force will be canceled by the horizontal tension created by the free falling mass of the upper-middle stick.

 

[Philip Wood]

The equations for 2-D rigid dynamics are

[itex]\sum[/itex]F_x = m[itex]\ddot{x}[/itex]

[itex]\sum[/itex]F_y = m[itex]\ddot{y}[/itex]

[itex]\sum[/itex]G = I[itex]\ddot{θ}[/itex]

in which [itex]\sum[/itex]F_x is the sum of x-components of force on the body, regardless of where on the body they act, and [itex]\ddot{x}[/itex] is the x-wise acceleration of the body's centre of mass.

Likewise for the y equation.

[itex]\sum[/itex]G is the sum of moments taken about the centre of mass for all forces acting on the body, I is the moment of inertia about the centre of mass and [itex]\ddot{θ}[/itex] is the angular acceleration of the body about its centre of mass.

 

[cshum00]

@Philip Wood
Please give me a fully layed-out equation using the components of the geometry not just the generic equations.

Edit: Nevermind, i calculated the torque myself.

First, let me define what is I or moment of intertia:[tex]\sum I = mr^2[/tex]Or, if M_c is the center of mass and r is constant:[tex]\sum m = M_c[/tex]Then,[tex]I = M_cr^2[/tex]

Then, substituting to your formula[tex]\sum G = \sum I \ddot{θ} = \sum M_cr^2 \ddot{θ} = \sum M_cr^2 \frac{a_t}{r} = \sum M_cra_t[/tex]

The tangent acceleration at the center of mass is:[tex]a_C = gcos(\theta)[/tex]
The tangent acceleration at point A is:[tex]a_A = \frac{Ncos(\theta)}{m}[/tex]

So, the torque is:[tex]\sum M_cra_t = Nr_n + F_cr_c = \tau[/tex][tex]\tau = Ncos(\theta)(0) + M_c gcos(\theta) \frac{\sqrt{2}}{2}[/tex][tex]\tau = \frac{\sqrt{2}M_cgcos(\theta)}{2}[/tex]Which implies that torque changes with the angle. Make sense because the normal force experienced at A changes with angle too. So the torque it creates is also varied.

Now that i got the torque, what else i need to come up with the kinematic equations to determine the positions of A, B or the center of mass at different angles θ?

 

[Philip Wood]

Probably not what you wanted...

 

[Philip Wood]

I'm a little worried about your a_c = g cos (θ), because your 'pivot', the left hand end of the rod, is accelerating to the left.

If you want to save some trouble (including one integration), abandon forces and torques and go straight for energy. Equate gravitational PE lost to sum of linear and rotational kEs. My equation was still nasty, though.

 

[cshum00]

Probably not what you wanted...

Not quite since you still left them in generic forms instead of using the values of the geometry; except for part (c) which you did more work.

Let's leave part (a) alone for now. We are assuming that there won't be any horizontal acceleration since we don't see any external horizontal force. But i would like to work on a proper proof later. Not just assumptions.As for part (b) you have:[tex]mg - F = m\ddot{y}[/tex]It is good for analyzing point A. Which is to allow the resulting vertical acceleration to be zero:[tex]mg - F = 0[/tex]
I don't like it very much if we use it to analyze the center of mass; because i don't see the internal forces. But if assuming that the internal forces cancel out we get:[tex]mg - 0 = m\ddot{y}[/tex][tex]mg = m\ddot{y}[/tex]Since the normal force F does not apply here.

But it certainly doesn't work at point B because we will get the same answer as analyzing the center of mass. Which cannot be true because B does fall down faster than the center of mass. Which implies that we must take the internal forces into account and analyze how the tension creates an additional downward force.

As for part (c), I am not sure how you derived your equation. But i am assuming that you are using the center of mass as pivoting point. On the other hand I am using point A as the pivoting point which moves to the left. But your pivoting point is not fixed neither because it moves downward.

So if i try to derive your formula you are using all three points:[tex]\sum M_cra_t = F_ar_a + F_cr_c + F_br_b = f \ddot{θ}[/tex][tex]Fcos(\theta) \frac{-L}{2} + M_cg(0) + m_bg \frac{L}{2} = f \ddot{θ}[/tex][tex]Fcos(\theta) \frac{L}{2} = m_bg \frac{L}{2} - f\ddot{θ}[/tex]Which i don't know how you concluded that:[tex]m_bg \frac{L}{2} - f\ddot{θ} = m \frac{L^2}{12} \ddot{θ}[/tex]But as you can see, if you use the center of mass as the pivoting point will make the center of mass disappear which is something we don't what at all.

I'm a little worried about your a_c = g cos (θ), because your 'pivot', the left hand end of the rod, is accelerating to the left.

Fixed. As you noticed, a_C has nothing to do with point A. For the tangent acceleration at point A see a_A.

If you want to save some trouble (including one integration), abandon forces and torques and go straight for energy. Equate gravitational PE lost to sum of linear and rotational kEs. My equation was still nasty, though.

I don't mind seeing those results as long as you show me the calculations. XD

 

[Philip Wood]

It seems – though I may have this wrong – that you are trying to apply equations to individual parts of the rod. No wonder you express disquiet at omitting internal forces (tensions etc.)!

The general dynamics I quoted earlier emerges from a treatment of rigid bodies which shows that if you consider the motion of the C of M and rotation about the C of M, then the internal forces don't need to be considered. This is not obvious or trivial. If you decide to use the rules couched in these terms (as I tried to do, however ineptly) then you mustn't try to apply equations to individual parts of the body; you can't switch back and forth from one approach to the other.

Anyway, I've done my best to help, and it clearly wasn't up to the mark. Good luck!

 

[cshum00]

It seems – though I may have this wrong – that you are trying to apply equations to individual parts of the rod. No wonder you express disquiet at omitting internal forces (tensions etc.)!

You are right. It took me some time to realize this too. When applying the problem to individual parts, it becomes thee different sub-problems. But i refuse that there isn't a simple neat answer. Something like F_x(r) or F_y(r) where r is the the point location of the stick. It might be somewhat difficult to reach there but i believe there is such answer.

Anyway, I've done my best to help, and it clearly wasn't up to the mark. Good luck!

Even so, thank you for all your help. You did help me advance and dig deeper on some parts. At least i got the torque thanks to you. And confirmed that the torque is not constant but variable with the angle.

 

[rcgldr]

That would be an internal compressive force

Yes and no. It a real situation, it is an internal compressible force.

I didn't use the term compressible, just compressive. Even if the idealized rod is incompressable, that doesn't mean it can't have internal pressures. My point here was that there are no external horizontal forces, so the center of mass will not accelerate horizontally.

I'm not sure if you can treat gravity as acting at the midpoint of the rod, but if it can, then the torque force equals upwards force at A times horizontal component of distance from A to midpoint of rod (actually 1/2 horizontal component of distance to midpoint x (upwards force at A + downwards force at midpoint (these forces are equal and opposing))).

The center of gravity is midpoint with no doubt.

I just wasn't sure if gravity can be considered as a vector force applied at the mid-point of the rod.

What we are not 100% so sure is whether it will fall down vertically.

Assuming that there is no initial horizontal component of velocity, then since there are no external horizontal forces, then the center of mass only moves and accelerates vertically. You could attach the end of the rod to massless pin that could slide freely in a horizontal slot, the rod could swing or rotate and the center of mass would not move horizontally, since there are no external horizontal forces.

solution

You should end up with two differential equations related to vertical acceleration of the center of mass with respect to the angle of the rod, one relating the upwards force from the frictionless surface at point A to vertical acceleration of center of mass, and the other relating acceleration of the center of mass to the angular acceleration of the rod due to the torque related to the upwards force (frictionless surface) at point A and downwards force (gravity) at the center of mass, divided by the angular inertia of a rod rotating about one end.

 

[cshum00]

I didn't use the term compressible, just compressive. Even if the idealized rod is incompressable, that doesn't mean it can't have internal pressures.

Whether it is "compressible" or "compressive", it is still about "compression" which means making it smaller to take less space. Although the action itself is compression, is still best to avoid the term.

I just wasn't sure if gravity can be considered as a vector force applied at the mid-point of the rod.

Well, center of mass/gravity 101. In a uniform, symmetric and rigid object, the center is always at the midpoint.

Assuming that there is no initial horizontal component of velocity, then since there are no external horizontal forces, then the center of mass only moves and accelerates vertically. You could attach the end of the rod to massless pin that could slide freely in a horizontal slot, the rod could swing or rotate and the center of mass would not move horizontally, since there are no external horizontal forces.

I am not sure how you can attach a pin that slides; and yet allow the end of the rod to move when there is a pin attached to it. Maybe you can draw me a picture to clarify.

You should end up with two differential equations related to vertical acceleration of the center of mass with respect to the angle of the rod, one relating the upwards force from the frictionless surface at point A to vertical acceleration of center of mass, and the other relating acceleration of the center of mass to the angular acceleration of the rod due to the torque related to the upwards force (frictionless surface) at point A and downwards force (gravity) at the center of mass, divided by the angular inertia of a rod rotating about one end.

What equations did you use? How did you end up with differential equations? Can you show me your calculations?

 

[rcgldr]

You could attach the end of the rod to massless pin that could slide freely in a horizontal slot, the rod could swing or rotate and the center of mass would not move horizontally, since there are no external horizontal forces.

I am not sure how you can attach a pin that slides; and yet allow the end of the rod to move when there is a pin attached to it.

As I mentioned, imagine the massless pin is bound on both sides by frictionless horizontal slots. Vertical motion of the pin is prevented, as well as motion in the direction of the pin, but there is no resistance (force) to horiztonal motion of the pin and the end of the rod the pin is attached to. It's bascially a pendulum with the pivot point free to move along a horiztonal line that is perpendicular to the axis of rotation of the pendulum. In this case the intial state is of an inverted pendulum.

You should end up with two differential equations related to vertical acceleration of the center of mass with respect to the angle of the rod, one relating the upwards force from the frictionless surface at point A to vertical acceleration of center of mass, and the other relating acceleration of the center of mass to the angular acceleration of the rod due to the torque related to the upwards force (frictionless surface) at point A and downwards force (gravity) at the center of mass, divided by the angular inertia of a rod rotating about one end.

What equations did you use? How did you end up with differential equations? Can you show me your calculations?

I didn't derive the equations, I just described them. Eventually you'll have equations that relate the acceleration of the center of mass versus angle of the rod. You'll need to integrate these equations (if they can be integrated) to calculate acceleration, velocity, position, and angle versus time.

 

[cshum00]

As I mentioned, imagine the massless pin is bound on both sides by frictionless horizontal slots. Vertical motion of the pin is prevented, as well as motion in the direction of the pin, but there is no resistance (force) to horiztonal motion of the pin and the end of the rod the pin is attached to. It's bascially a pendulum with the pivot point free to move along a horiztonal line that is perpendicular to the axis of rotation of the pendulum. In this case the intial state is of an inverted pendulum.

A picture is worth a thousand words. You are confusing me more now that you are relating it to a pendulum. Just draw me a picture please.

I didn't derive the equations, I just described them. Eventually you'll have equations that relate the acceleration of the center of mass versus angle of the rod. You'll need to integrate these equations (if they can be integrated) to calculate acceleration, velocity, position, and angle versus time.

How can you be sure what the outcome of the equations will be if you didn't derive them? Sorry but baseless proof is meaningless for me.

 

[Philip Wood]

As threatened earlier, here's the energy treatment of the problem. Much easier to formulate the equation to be solved.

I did differentiate it wrt t to check that it agreed with my forces and torques treatment (thumbnail in post 20) and it does – except for a slipped sign in that thumbnail.

 

[cshum00]

As threatened earlier, here's the energy treatment of the problem. Much easier to formulate the equation to be solved.

I love your work this time because i am able to understand 90% of your calculations. I still need some clarifications though. Please help me to understand.

It took me some time to understand but it seems that you love the dot derivative notation to indicate velocity and acceleration. So now that is out of the way, i wonder how you calculate your radius.

In the transnational kinetic energy part, you seemed to have chosen a variable radius. This radius you have chosen is always the x-projection between point A and the center of mass. This is why you got:[tex]\frac{Lcos\theta}{2}[/tex]
But then the radius you have chosen for the rotational kinetic energy is different. And i don't know how you came up with:[tex]\frac{L}{\sqrt{12}}[/tex]
Which also makes me wonder, what is your pivot point? Why there are two different radius? Shouldn't the pivot point be point A and the radius just L/2?

 

[Philip Wood]

Don't think about it in terms of radius and pivot point.

You agree that y = [itex]\frac{L}{2}[/itex]sin[itex]\theta[/itex] ?

In that case [itex]\dot{y}[/itex] = [itex]\frac{L}{2}[/itex]cos[itex]\theta[/itex] [itex]\dot{θ}[/itex].

The rotational KE must be calculated about the centre of mass (CM). The formula for rotational KE is [itex]\frac{1}{2}[/itex]Iω². I, the moment of inertia of the rod about its centre, is [itex]\frac{1}{12}[/itex]mL².

But ω = [itex]\dot{θ}[/itex], the rate of change of the angle θ shown on the diagram.

Hope it all makes sense now.

 

[cshum00]

You agree that y = [itex]\frac{L}{2}[/itex]sin[itex]\theta[/itex] ?

In that case [itex]\dot{y}[/itex] = [itex]\frac{L}{2}[/itex]cos[itex]\theta[/itex] [itex]\dot{θ}[/itex].

Interesting. You derived velocity by calculating the derivative of y. I did it differently. I substituted the relationship between velocity, radius and angular velocity like this: [itex]\dot{y} = r \dot{\theta}[/itex]. Then you can compare both results and see that that [itex]\frac{L}{2}[/itex]cos[itex]\theta[/itex] happens to be your radius for angular the velocity. And according to the physical geometry, it is the projection between point A and the center of mass in the x-axis.

The rotational KE must be calculated about the centre of mass (CM). The formula for rotational KE is [itex]\frac{L}{2}[/itex]Iω².

I think it was a typo and you meant that the rotational KE is [itex]\frac{1}{2}[/itex]Iω²

I, the moment of inertia of the rod about its centre, is [itex]\frac{1}{12}[/itex]mL².

Let's define moment of inertia again: [itex]I = mr^2[/itex].
So, if [itex]I = m(\frac{L^2}{12})[/itex], means your radius is [itex]\frac{L}{\sqrt{12}}[/itex]. How come?

 

[Philip Wood]

Sorry about the typo.

[itex]\frac{L}{\sqrt{12}}[/itex] is what's called the 'radius of gyration' of the rod about its centre. The interpretation is this: if all the rod's mass were to be gathered together at one point, then if that point were to be at the radius of gyration from the rod's centre, then the rod would have the same moment of inertia about its centre as the original rod.

Do you, I wonder, need to learn up about moment of inertia: (a) its rôle in mechanics, and (b) how to calculate moments of inertia of a few simple bodies, like cylinders and rods? Sorry if this seems patronising, but you do seem very keen to get to the bottom of this stuff.

 

[rcgldr]

angular inertia of a rod rotating about one end.

That should have been rod rotating by it's center, since the end of the rod is not constrained horizontally (frictionless surface) and the center of mass moves and acceleates only vertically. Philip Wood already did the math using angular inertia for a rod rotating about it's center.

The 'radius of gyration' of the rod about its centre. The interpretation is this: if all the rod's mass were to be gathered together at one point ...

or all the mass located in a hollow cylinder at that radius of gyration, or any collection of point masses, as long as all of them are located at the radius of gyration.

 

[cshum00]

Sorry if this seems patronising, but you do seem very keen to get to the bottom of this stuff.

Of course i am. I am sure you didn't pick that value for radius of gyration randomly. I want to be able to understand the calculations myself.

[itex]\frac{L}{\sqrt{12}}[/itex] is what's called the 'radius of gyration' of the rod about its centre.

I found how the number was obtained. It seems that i was just picking a radius away from my chosen pivot point; which is wrong? It seems that we have to calculate this radius by integrating the stick.
[itex]dm = \frac{M}{L}dr[/itex]
[itex]I = \int_{\frac{-L}{2}}^{\frac{L}{2}} r^2 dm = \frac{M}{L} \int_{\frac{-L}{2}}^{\frac{L}{2}} r^2dr[/itex]
[itex]I = \frac{M}{L} \frac{r^3}{3} |_{\frac{-L}{2}}^{\frac{L}{2}} = \frac{M}{3L} (\frac{L^3}{8} + \frac{L^3}{8}) = M \frac{L^2}{12}[/itex]

However, i question that if finding the radius of gyration this way is really correct? Here is a simple example i am going to use. Assume that our problem, point A is a fixed pivot point. And i am going to try to find the torque of the stick when gravity is the only relevant force.
[itex]\tau = \alpha I = \frac{a_t}{r} mr^2 = F_t r[/itex]

-First, let's calculate the inertia and radius of gyration; with the fixed pivot point A. So the points of integration are from 0 to L.
[itex]I = \int_{0}^{L} r^2 dm = \frac{M}{L} \int_{0}^{L} r^2dr = \frac{M}{L} \frac{r^3}{3} |_{0}^{L} = \frac{M}{3L} (L^3 - 0) = M \frac{L^2}{3}[/itex]
-Therefore the radius of gyration when the pivot is at the end of the stick is: [itex]\frac{L}{\sqrt{3}}[/itex]
-The tangent acceleration that can be obtained by the geometry is equals: [itex]a_t = -gcos(\theta)[/itex]
-Then the torque equals: [itex]\tau = \alpha I = \frac{-gcos(\theta)}{\frac{L}{\sqrt{3}}}M \frac{L^2}{3} = \frac{-\sqrt{3}LMgcos(\theta)}{3}[/itex]
-But the torque is also equals: [itex]\tau = F_t r = -Mgcos(\theta) \frac{L}{2}[/itex]
-Or even if i use the radius of gyration instead of a distance between the pivot and the center of mass: [itex]\tau = F_t r = -Mgcos(\theta) \frac{L}{\sqrt{3}}[/itex]
-Even if i do a mix and match on the torque that contains moment of inertia: [itex]\tau = \alpha I = \frac{-gcos(\theta)}{\frac{L}{2}}M \frac{L^2}{3} = \frac{-2LMgcos(\theta)}{3}[/itex]

One last thing, it took me to try it with a different notation to actually find out that this is wrong:

You agree that y = [itex]\frac{L}{2}[/itex]sin[itex]\theta[/itex] ?

In that case [itex]\dot{y}[/itex] = [itex]\frac{L}{2}[/itex]cos[itex]\theta[/itex] [itex]\dot{θ}[/itex].

This is what you are doing:
[itex]x = y^2[/itex]
[itex]\frac{dx}{dz} = \frac{d}{dz}(y^2) = 2y \frac{dy}{dz}[/itex] which is wrong