- #1
Karol
- 1,380
- 22
Homework Statement
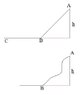
There is an inclined path like in the upper drawing. a mass is released at height h (point A) and the mass slides until it stops on the horizontal surface at C. the energy required to drag it up again to A is 2mgh.
Now the path is curved like in the lower drawing but in this case we don't know what is the energy required to drag it up again to A. why?
Homework Equations
Friction force: $$F=mg\mu$$
The Attempt at a Solution
My explanation to the first situation with the straight inclined path is that there is a constant ratio between each meter of sliding along the path to the decrease in height, i mean every meter the mass advances consumes, let's say, 0.8 meter of vertical height. the first mgh is needed to overcome the friction and the second mgh in order to lift it.
But even if this ratio changes in case of the curved path, still the mass stops after it consumed energy oh height h, so why isn't the same answer 2mgh hold here?