Fourier Transform Scaling Property help

[Uan]

Hi,

I'm following the proof of the "Scaling Property of the Fourier Transform" from here:

http://www.thefouriertransform.com/transform/properties.php

...but don't understand how they went from the integral to the right hand term here:

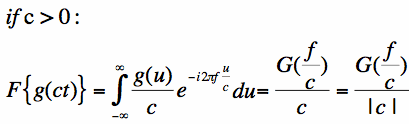
The definition of the Fourier Trasform they use is this:

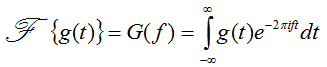
Thanks,
Uan

 

[vanhees71]

I don't understand, where there is a problem, because it's simply the definition of the Fouier transform. The full calculation goes as follows. We start with the definition of the Fourier transform:
[tex]\mathcal{F}\{g(c t)\}=\int_{\mathbb{R}} \mathrm{d t} g(t) \exp[-2 \pi \mathrm{i} f t].[/tex]
Now we substitute [itex]u=c t[/itex], which gives
[tex]\mathcal{F}\{g(c t)\}=\frac{1}{|c|} \int_{\mathbb{R}} \mathrm{d} t \exp[-2 \pi \mathrm{i} u (f/c)]=\frac{1}{|c|} G(f/c),[/tex]
where
[tex]G(f)=\mathcal{F}\{g(t)\}(f).[/tex]

 

[Uan]

I don't understand, where there is a problem, because it's simply the definition of the Fouier transform. The full calculation goes as follows. We start with the definition of the Fourier transform:
[tex]\mathcal{F}\{g(c t)\}=\int_{\mathbb{R}} \mathrm{d t} g(t) \exp[-2 \pi \mathrm{i} f t].[/tex]
Now we substitute [itex]u=c t[/itex], which gives
[tex]\mathcal{F}\{g(c t)\}=\frac{1}{|c|} \int_{\mathbb{R}} \mathrm{d} t \ exp[-2 \pi \mathrm{i} u (f/c)]=\frac{1}{|c|} G(f/c),[/tex]
where
[tex]G(f)=\mathcal{F}\{g(t)\}(f).[/tex]

Hi vanhees71,

I get the substitution but I don't see how they went from the integral to the next bit. To me, the form of the integral doesn't quite match the definition in my first post, it has got g(u) but the exponential has exp(-i*2*pi*f*(u/c)), so this is where I get hung up...

Needs to be [STRIKE]either[/STRIKE] g(u/c) [STRIKE][or exp(-i*2*pi*f*u)^(1/c) ? ] (sorry forget this)[/STRIKE] or something to be able to apply the definition. Feels like I'm missing something simple.

One more thing, are you missing g(ct) from your first integral and g(u) on your second integral?

[tex]\mathcal{F}\{g(c t)\}=\int_{\mathbb{R}} \mathrm{d t} g(c t) \exp[-2 \pi \mathrm{i} f t].[/tex]

[tex]\mathcal{F}\{g(c t)\}=\frac{1}{|c|} \int_{\mathbb{R}} \mathrm{d} t \ g(u) exp[-2 \pi \mathrm{i} u (f/c)]=\frac{1}{|c|} G(f/c),[/tex]

 

[jbunniii]

Hi vanhees71,

I get the substitution but I don't see how they went from the integral to the next bit. To me, the form of the integral doesn't quite match the definition in my first post, it has got g(u) but the exponential has exp(-i*2*pi*f*(u/c)), so this is where I get hung up...

Start with the definition of the Fourier transform:
$$G(f) = \int_{-\infty}^{\infty} g(u) \exp[-2\pi i f u] du$$
Now substitute ##f/c## in place of ##f##:
$$G(f/c) = \int_{-\infty}^{\infty} g(u) \exp[-2\pi i (f/c) u] du$$
Multiply by ##1/c##:
$$\frac{1}{c} G(f/c) = \int_{-\infty}^{\infty} \frac{g(u)}{c} \exp[-2\pi i (f/c) u] du$$
which is the second equality in your displayed equation.

 

[Uan]

Start with the definition of the Fourier transform:
$$G(f) = \int_{-\infty}^{\infty} g(u) \exp[-2\pi i f u] du$$
Now substitute ##f/c## in place of ##f##:
$$G(f/c) = \int_{-\infty}^{\infty} g(u) \exp[-2\pi i (f/c) u] du$$
Multiply by ##1/c##:
$$\frac{1}{c} G(f/c) = \int_{-\infty}^{\infty} \frac{g(u)}{c} \exp[-2\pi i (f/c) u] du$$
which is the second equality in your displayed equation.

Cheers jbunniii, just what I was after! :thumbs: