- #1
robertjford80
- 388
- 0
Homework Statement
The Attempt at a Solution
I don't understand where that 2 comes from in the denominator in cos nπ/2
robertjford80 said:Homework Statement
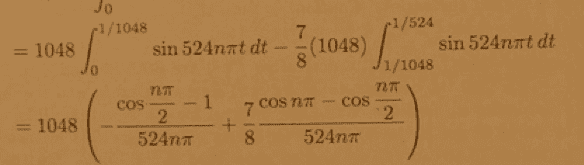
The Attempt at a Solution
I don't understand where that 2 comes from in the denominator in cos nπ/2
robertjford80 said:of course i always do my own derivation. my own derivation is -cosnπ/524nπ - 1/524nπ
There, I'm still as clueless I was before.
A Fourier series is a mathematical representation of a periodic function in terms of a sum of sine and cosine waves. It allows for the decomposition of a complex signal into simpler components, making it easier to analyze and understand.
A Fourier series is commonly used in sound engineering to analyze and manipulate sound waves. By breaking down a sound wave into its individual frequency components, we can understand how different frequencies contribute to the overall sound and make adjustments as needed.
Some common applications of Fourier series in sound include noise reduction, equalization, and synthesis. By understanding the frequency components of a sound, we can apply filters and effects to manipulate the sound in various ways.
One limitation of Fourier series is that it assumes the signal is periodic, which is not always the case in sound. This can lead to inaccuracies in the analysis of non-periodic sounds. Additionally, Fourier series does not take into account factors such as timbre and envelope, which are important in describing the quality and character of a sound.
The use of Fourier series in sound has evolved significantly with advancements in technology. In the past, it was primarily used for basic analysis and manipulation of sound waves. Now, it is used in more complex algorithms for tasks such as speech recognition and audio compression. It has also been combined with other mathematical techniques, such as wavelets, to improve its accuracy and functionality.