- #1
member 428835
hi PF! I've attached pictures to help you all see what is happening. Basically, I am running a forward time-centered space finite difference scheme, which is $${h_i^{j+1} \approx \left[ h_i^j \left( \frac{h_{i+1}^j-2h_i^j+h_{i-1}^j}{\Delta z^2} \right) + \frac{1}{2}\left( \frac{h_{i+1}^{j}-h_{i-1}^j}{ \Delta z} \right)^2 \right]\Delta t+h_i^j}.$$ The system runs fine as long as my final run time ##tf## is low. Since ##\Delta t## is defined as ##tf/M^2## where ##M## is the number of spatial nodes (determined by scaling, which I know is accurate).
At any rate, the following pictures are from the same number of time iterations, but different the divergent picture has a much larger ##tf## value. Any idea why one diverges and the other maintains equilibrium? I know ##tf## is the reason, but why?
Thanks so much!
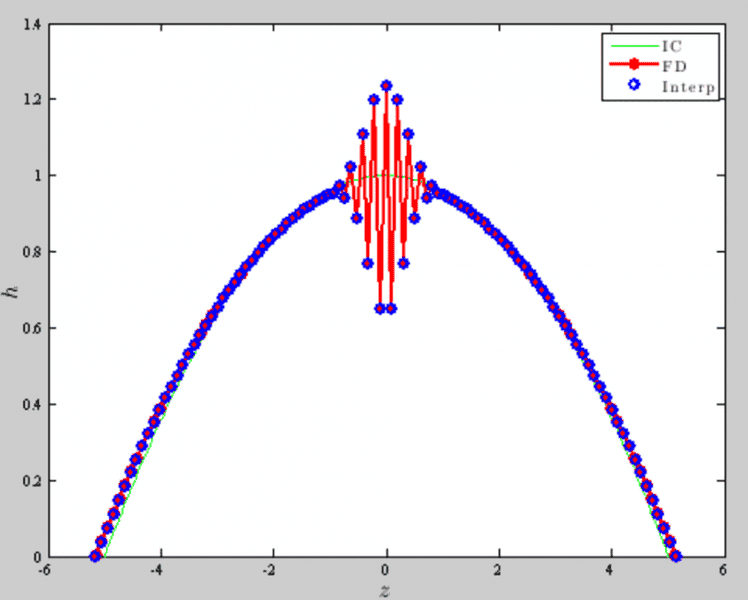
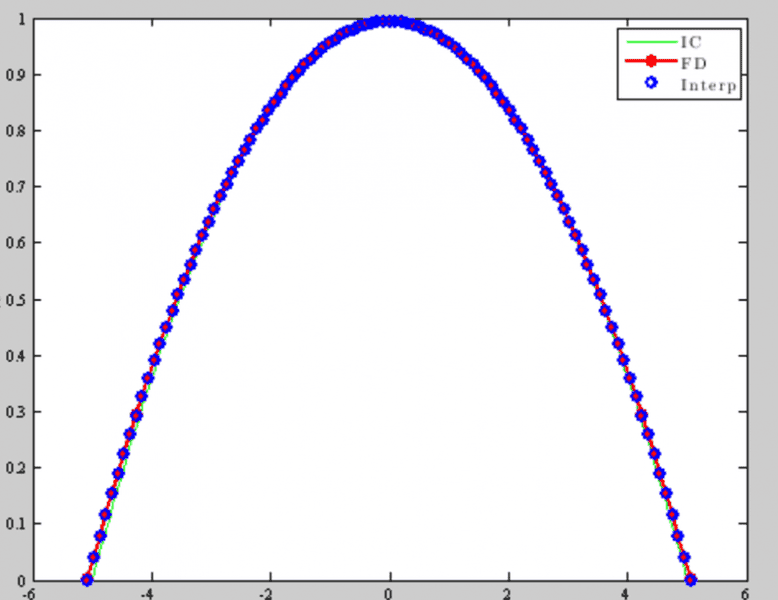
At any rate, the following pictures are from the same number of time iterations, but different the divergent picture has a much larger ##tf## value. Any idea why one diverges and the other maintains equilibrium? I know ##tf## is the reason, but why?
Thanks so much!