- #1
ruu
- 2
- 0
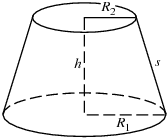
Mt. Vesuvius in Pompeii was a conic volcano with a height from its base 7950 feet and a base radius of 2300 feet. In 79 AD, the volcano erupted, reducing its height to 4200 feet . Find the volume of the volcano after 79 AD in terms of pi.
WORK:
Volume of Volcano(Before 79AD)= \pi *r^2*h/3
=\pi *(2300)^2 * 7950/3
=5290000\pi * 2650
= 1.4019 * 10^10 * \pi
Volume of Volcano part erupted off:
Height: 7950 ft - 2300 ft = 5650 ft
Radius= 5650 * (2300/7950) = 1634.5912 ft
Volume= \pi *r^2*h/3
= \pi *(1634.5912)^2*5650/3
=2671888.375 \pi * 1896.6667
=5067681707* \pi
Volume of Volcano(After 79AD)= (Volume of Volcano(Before 79AD)) - (Volume of Volcano part erupted off)
=(1.4019 * 10^10 * \pi) - (5067681707* \pi)
= 8951318293* \pi
Note to reader: Please check my work. I'm not sure if my solutions are correct or if i did the problem correctly.
Thank you!
WORK:
Volume of Volcano(Before 79AD)= \pi *r^2*h/3
=\pi *(2300)^2 * 7950/3
=5290000\pi * 2650
= 1.4019 * 10^10 * \pi
Volume of Volcano part erupted off:
Height: 7950 ft - 2300 ft = 5650 ft
Radius= 5650 * (2300/7950) = 1634.5912 ft
Volume= \pi *r^2*h/3
= \pi *(1634.5912)^2*5650/3
=2671888.375 \pi * 1896.6667
=5067681707* \pi
Volume of Volcano(After 79AD)= (Volume of Volcano(Before 79AD)) - (Volume of Volcano part erupted off)
=(1.4019 * 10^10 * \pi) - (5067681707* \pi)
= 8951318293* \pi
Note to reader: Please check my work. I'm not sure if my solutions are correct or if i did the problem correctly.
Thank you!
Last edited: