- #1
Kaushik
- 282
- 17
Consider a purely inductive circuit with an inductor of self-inductance ##L## and sinusoidally varying AC source of peak voltage ##V_{m}##.
First of all, Why is ##V_{ac} = ε_{ind}## (where ##ε_{ind}## is the back emf)?
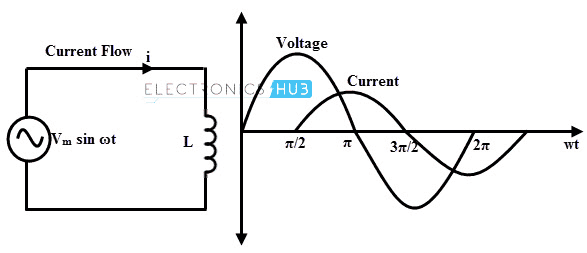
Now, at ## t=0 ##, voltage is increasing at a fast rate. Hence, due to the sudden increase in current, the inductor induces maximum back emf (in the opposite direction) and current is maximum in the opposite direction.
Now, at ## t = T/4## (where ## T## is the time period), Voltage is maximum and not changing much. Now, this is where I think I'm going wrong. I am interpreting this as '##I## is not changing much because ##V##, when maximum, is not changing much (##\frac{dV}{dt} = 0##). Why is it wrong?
Interpreting it in the same way, when ##t = T/2##,## V = 0##. and ##\frac{dV}{dt} = -1##. So, the current is also changing at a fast rate. Due to this, there is a back emf induced that opposes the change in current. But here, Current is reducing rapidly. So, back emf is induced to increase the current in a positive direction.
I feel like I am misinterpreting it here: I am thinking of ##\frac{dV}{dt}## as the rate at which current is changing. And from the graph, it is quite evidently not the case. But, I can't find the reason as to why it is not the case intuitively?
I hope you got my question. If not, I apologise. Feel free to ask questions regarding 'my question'.
I am confused
First of all, Why is ##V_{ac} = ε_{ind}## (where ##ε_{ind}## is the back emf)?
Now, at ## t=0 ##, voltage is increasing at a fast rate. Hence, due to the sudden increase in current, the inductor induces maximum back emf (in the opposite direction) and current is maximum in the opposite direction.
Now, at ## t = T/4## (where ## T## is the time period), Voltage is maximum and not changing much. Now, this is where I think I'm going wrong. I am interpreting this as '##I## is not changing much because ##V##, when maximum, is not changing much (##\frac{dV}{dt} = 0##). Why is it wrong?
Interpreting it in the same way, when ##t = T/2##,## V = 0##. and ##\frac{dV}{dt} = -1##. So, the current is also changing at a fast rate. Due to this, there is a back emf induced that opposes the change in current. But here, Current is reducing rapidly. So, back emf is induced to increase the current in a positive direction.
I feel like I am misinterpreting it here: I am thinking of ##\frac{dV}{dt}## as the rate at which current is changing. And from the graph, it is quite evidently not the case. But, I can't find the reason as to why it is not the case intuitively?
I hope you got my question. If not, I apologise. Feel free to ask questions regarding 'my question'.
I am confused
