- #1
Ren Figueroa
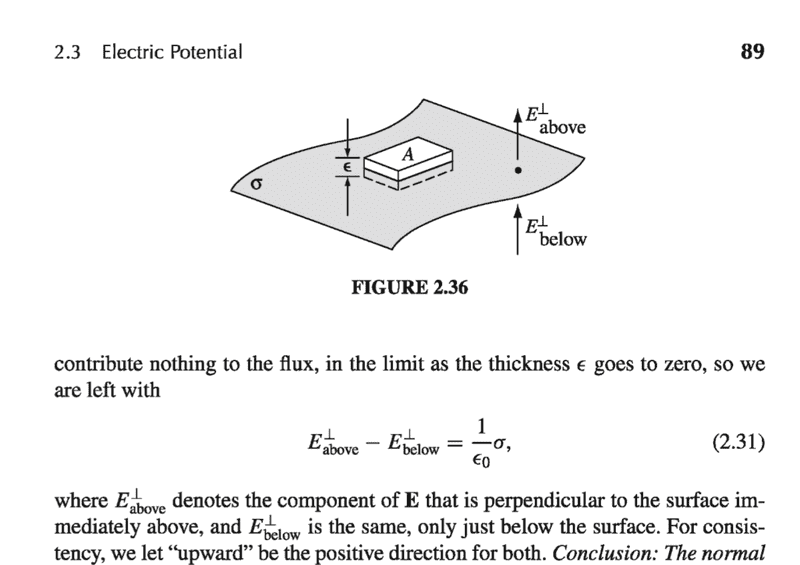
Hi. I'm going over the discontinuity aspects of the electric field as we cross the surface charge. A pillbox Gaussian surface was drawn and the electric field for "below" is throwing me off. Can someone explain why the electric field is pointing in the same direction from both sides of the surface? I supplied the image below. Thanks!