- #1
keenPenguin
- 21
- 3
Hello,
I couldn't figure out the following problem so far.
[tex]m,n \in \mathbb{N}[/tex]. Show the following relations:
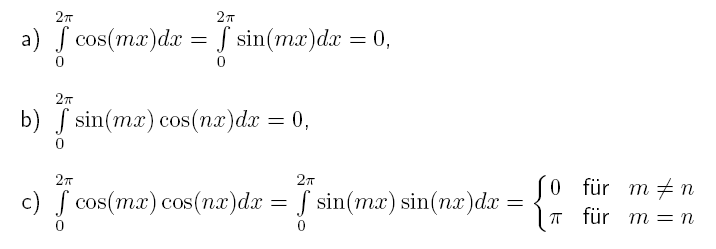
a) is no problem, but b) and c) seem tricky. I tried partial integration (two times) on b), which gave me a term which contained the original integral. So I sorted the term and got that:
[tex]\int_{0}^{2\pi}\sin\left(mx\right)\cos\left(nx\right)dx=\frac{1}{1+\frac{n^{2}}{m^{2}}}\left(\left[-\frac{\cos\left(mx\right)}{m}\cos\left(nx\right)\right]_{0}^{2\pi}+\frac{n}{m}\left[\frac{\sin\left(mx\right)}{m}\sin\left(nx\right)\right]_{0}^{2\pi}\right)[/tex]
But I can't see why this should be zero.
Any help appreciated!
kP
I couldn't figure out the following problem so far.
Homework Statement
[tex]m,n \in \mathbb{N}[/tex]. Show the following relations:
Homework Equations
a) is no problem, but b) and c) seem tricky. I tried partial integration (two times) on b), which gave me a term which contained the original integral. So I sorted the term and got that:
[tex]\int_{0}^{2\pi}\sin\left(mx\right)\cos\left(nx\right)dx=\frac{1}{1+\frac{n^{2}}{m^{2}}}\left(\left[-\frac{\cos\left(mx\right)}{m}\cos\left(nx\right)\right]_{0}^{2\pi}+\frac{n}{m}\left[\frac{\sin\left(mx\right)}{m}\sin\left(nx\right)\right]_{0}^{2\pi}\right)[/tex]
But I can't see why this should be zero.
Any help appreciated!
kP