- #1
TheCanadian
- 367
- 13
Hi there, I was just trying to perform a change of variable on a differential equation as shown below. The original second order ODE is written in terms of a dependent variable ## \theta ## and independent variable ##q##. I have used the expression ## q = \sqrt{\frac{z\tau'}{LT_R}} ## and ##\tau' = T'(1-e^{\frac{-\tau}{T'}}) ## (where ##z## and ##\tau## are also independent variables, while ##L, T',## and ##T_R## are known constants). I am only considering the case of ##z = 0.01L## and am thus only solving this equation for a varying ##\tau##. (In this case, ##\tau## is a purely real and positive number.) I have posted my work below to transform the second order ODE into a function of ##t## instead of ##q##. (I may have used ##t## and ##\tau## interchangeably out of bad habit--my apologies if this causes confusion.) If you could possibly check it to see if there are any errors, that would be greatly appreciated as I'm still a little uncertain if I've applied the chain rule correctly in certain parts.
(My apologies if this is the wrong section to post such question, although this is not homework.)
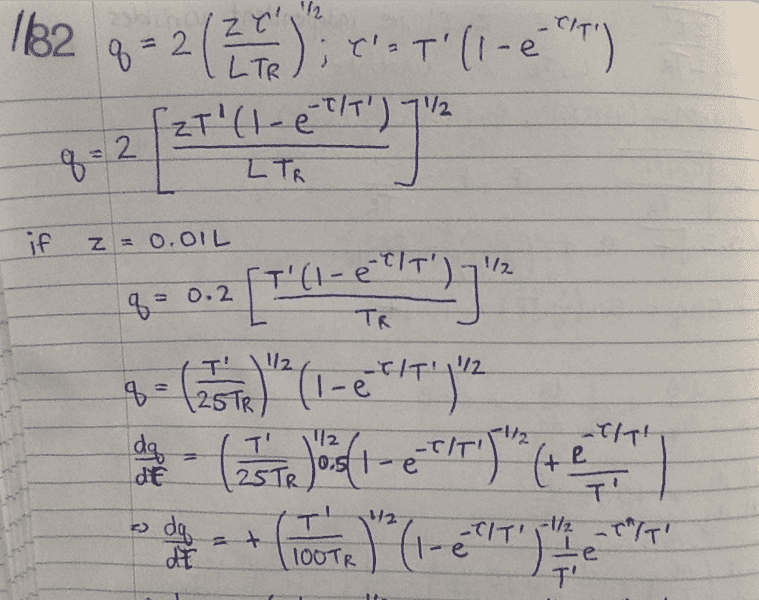
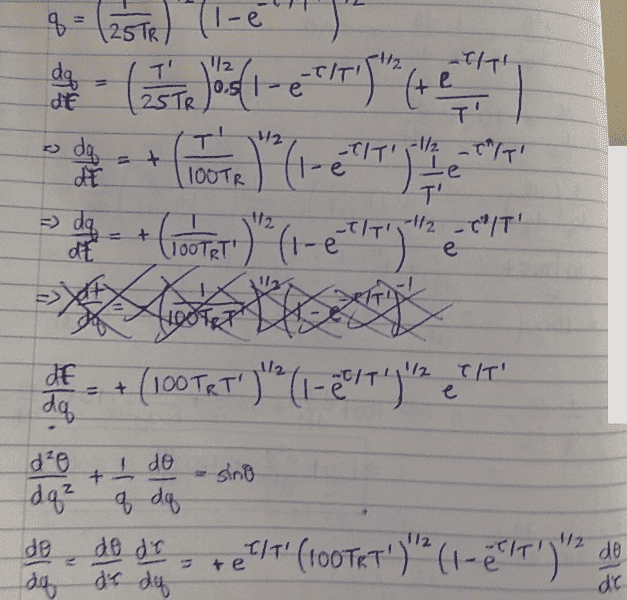
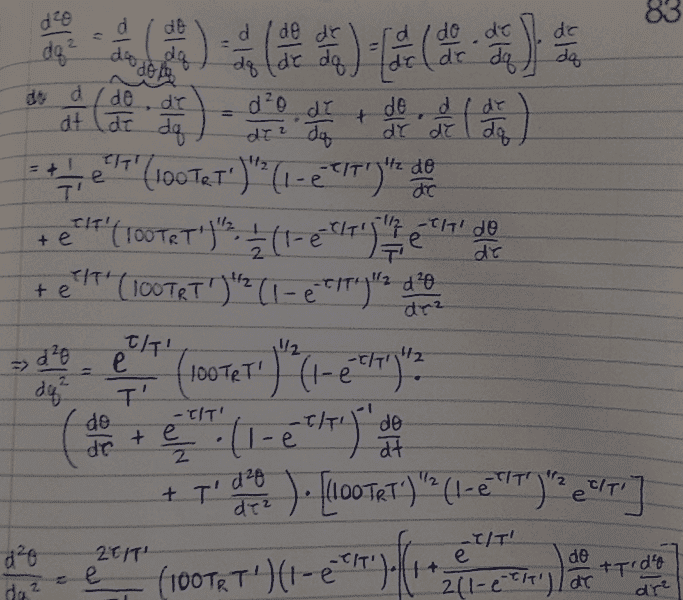
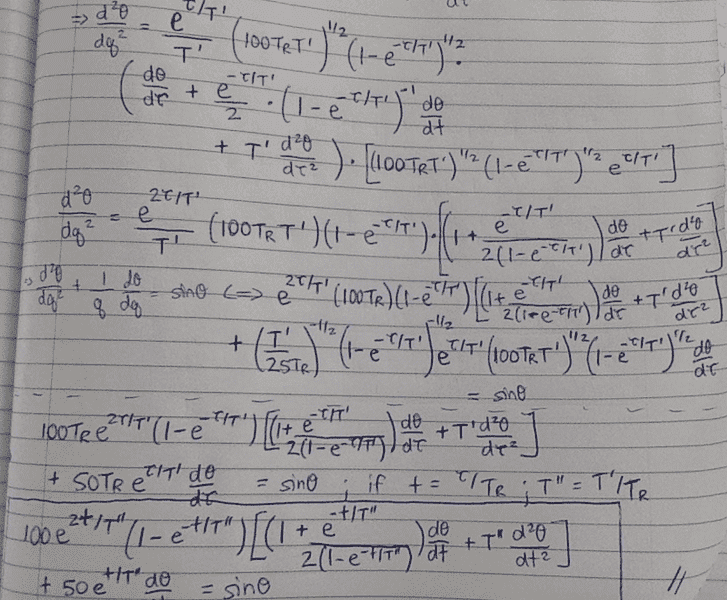
The final solution I get (it is partially cut in the last image) is:
$$ 100e^{\frac{2t}{T''}}(1-e^{\frac{-t}{T''}})[(1 + \frac {e^{\frac{-t}{T''}}}{2(1-e^{\frac{-t}{T''}})}) \frac {d\theta}{dt} + T'' \frac {d^2\theta}{dt^2} ] + 50e^{\frac{t}{T''}}\frac {d\theta}{dt} = sin(\theta) $$
which can also be expressed as:
$$ 100T''(e^{\frac{2t}{T''}}-e^{\frac{t}{T''}}) \frac {d^2\theta}{dt^2} + 50e^{\frac{t}{T''}}[(e^{\frac{t}{T''}}-1)(2+ \frac {1}{e^{\frac{t}{T''}}-1}) + 1]\frac {d\theta}{dt} = sin(\theta) $$
which is equivalent to:
$$ 100T''(e^{\frac{2t}{T''}}-e^{\frac{t}{T''}}) \frac {d^2\theta}{dt^2} + 100e^{\frac{2t}{T''}}\frac {d\theta}{dt} = sin(\theta) $$
(My apologies if this is the wrong section to post such question, although this is not homework.)
The final solution I get (it is partially cut in the last image) is:
$$ 100e^{\frac{2t}{T''}}(1-e^{\frac{-t}{T''}})[(1 + \frac {e^{\frac{-t}{T''}}}{2(1-e^{\frac{-t}{T''}})}) \frac {d\theta}{dt} + T'' \frac {d^2\theta}{dt^2} ] + 50e^{\frac{t}{T''}}\frac {d\theta}{dt} = sin(\theta) $$
which can also be expressed as:
$$ 100T''(e^{\frac{2t}{T''}}-e^{\frac{t}{T''}}) \frac {d^2\theta}{dt^2} + 50e^{\frac{t}{T''}}[(e^{\frac{t}{T''}}-1)(2+ \frac {1}{e^{\frac{t}{T''}}-1}) + 1]\frac {d\theta}{dt} = sin(\theta) $$
which is equivalent to:
$$ 100T''(e^{\frac{2t}{T''}}-e^{\frac{t}{T''}}) \frac {d^2\theta}{dt^2} + 100e^{\frac{2t}{T''}}\frac {d\theta}{dt} = sin(\theta) $$
Last edited: