- #1
orlan2r
- 31
- 0
A hemisphere of 8 kg mass and 20 cm radius is at the bottom of a tank containing water. Find out the minimum work that an agent must to do to extract the hemisphere of the water.(g = 10 m/s2)
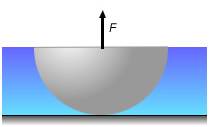
Please help me
Please help me